
题目列表(包括答案和解析)
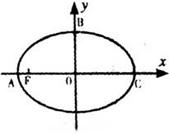
(14分)已知椭圆![]() 的左焦点为
的左焦点为![]() ,左右顶点分别为
,左右顶点分别为![]() ,
,![]() ,上顶点为
,上顶点为![]() ,过
,过![]() ,
,![]() 三点作⊙M,其中圆心
三点作⊙M,其中圆心![]() 的坐标为(
的坐标为(![]() )。
)。
(I)若⊙M的圆心在直线![]() 上,求椭圆
上,求椭圆![]() 的方程。
的方程。
(Ⅱ)若![]() 、
、![]() 是椭圆
是椭圆![]() 上满足
上满足![]() 的两点,求证:
的两点,求证:![]() 是定值。
是定值。
(14分)已知椭圆![]() 的左焦点为
的左焦点为![]() ,左右顶点分别为
,左右顶点分别为![]() ,
,![]() ,上顶点为
,上顶点为![]() ,过
,过![]() ,
,![]() 三点作⊙M,其中圆心
三点作⊙M,其中圆心![]() 的坐标为(
的坐标为(![]() )。
)。
(I)若![]() 是⊙M的直径,求椭圆的离心率;
是⊙M的直径,求椭圆的离心率;
(Ⅱ)若⊙M的圆心在直线![]() 上,求椭圆的方程。
上,求椭圆的方程。

已知椭圆![]() 的左焦点为
的左焦点为![]() ,左右顶点分别为
,左右顶点分别为![]() ,上顶点为
,上顶点为![]() ,过
,过![]() 三点作圆
三点作圆![]() ,其中圆心
,其中圆心![]() 的坐标为
的坐标为![]() .
.
(Ⅰ)当![]() 时,椭圆的离心率的取值范围.
时,椭圆的离心率的取值范围.
(Ⅱ)直线![]() 能否和圆
能否和圆![]() 相切?证明你的结论.
相切?证明你的结论.
已知椭圆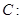
 的左焦点为
的左焦点为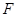 ,左、右顶点分别为
,左、右顶点分别为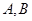 ,过点
,过点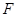 且倾斜角为
且倾斜角为 的直线
的直线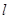 交椭圆于
交椭圆于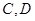 两点,椭圆
两点,椭圆 的离心率为
的离心率为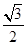 ,
,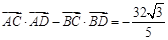 .
.
(1)求椭圆 的方程;
的方程;
(2)若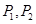 是椭圆上不同两点,
是椭圆上不同两点,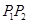
 轴,圆
轴,圆 过点
过点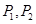 ,且椭圆上任意一点都不在圆
,且椭圆上任意一点都不在圆 内,则称圆
内,则称圆 为该椭圆的内切圆.问椭圆
为该椭圆的内切圆.问椭圆 是否存在过点
是否存在过点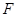 的内切圆?若存在,求出点
的内切圆?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
已知椭圆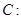
 的左焦点为
的左焦点为 ,左、右顶点分别为
,左、右顶点分别为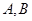 ,过点
,过点 且倾斜角为
且倾斜角为 的直线
的直线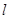 交椭圆于
交椭圆于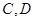 两点,椭圆
两点,椭圆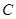 的离心率为
的离心率为 ,
, .
.
(1)求椭圆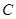 的方程;
的方程;
(2)若 是椭圆上不同两点,
是椭圆上不同两点,
 轴,圆
轴,圆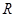 过点
过点 ,且椭圆上任意一点都不在圆
,且椭圆上任意一点都不在圆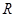 内,则称圆
内,则称圆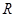 为该椭圆的内切圆.问椭圆
为该椭圆的内切圆.问椭圆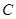 是否存在过点
是否存在过点 的内切圆?若存在,求出点
的内切圆?若存在,求出点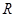 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.B 2.A 3.B 4.B 5.C 6.B 7.D 8.C 9.D 10.A 11.C 12.A
二、填空题(本大题共4小题,每小题4分,共16分)
13.试卷.files/image311.gif) 14.18
15.
14.18
15.试卷.files/image183.gif) 、
、试卷.files/image179.gif) 、
、试卷.files/image181.gif) 16.
16.试卷.files/image316.gif)
三、解答题(本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。)
17.解:(Ⅰ)试卷.files/image318.gif)
=试卷.files/image320.gif)
试卷.files/image322.gif) 函数
函数试卷.files/image200.gif) 的周期
的周期试卷.files/image325.gif) ,
,
由题意可知试卷.files/image327.gif) 即
即试卷.files/image329.gif) ,
,
解得试卷.files/image331.gif) ,即
,即试卷.files/image204.gif) 的取值范围是
的取值范围是试卷.files/image334.gif)
(Ⅱ)由(Ⅰ)可知试卷.files/image336.gif)
而试卷.files/image338.gif)
由余弦定理知试卷.files/image340.gif)
试卷.files/image342.gif) 又
又试卷.files/image344.gif) ,
,试卷.files/image346.gif)
试卷.files/image347.jpg)
试卷.files/image349.gif)
18.(I)证明:连结试卷.files/image351.gif) 交
交试卷.files/image353.gif) 于
于试卷.files/image355.gif) ,连结
,连结试卷.files/image357.gif)
试卷.files/image359.gif) 底面
底面试卷.files/image219.gif) 是正方形,
是正方形,试卷.files/image362.gif) 点
点试卷.files/image364.gif) 是
是试卷.files/image366.gif) 的中点,
的中点,
在试卷.files/image368.gif) 中,
中,试卷.files/image357.gif) 是中位线,
是中位线,试卷.files/image371.gif) ,
,
而试卷.files/image373.gif) 平面
平面试卷.files/image375.gif) 且
且试卷.files/image377.gif) 平面
平面试卷.files/image375.gif) ,所以,
,所以,试卷.files/image235.gif) 平面
平面试卷.files/image375.gif)
(Ⅱ)证明:试卷.files/image382.gif) 底面
底面试卷.files/image219.gif) 且
且试卷.files/image385.gif) 底面
底面试卷.files/image387.gif) ,
,
试卷.files/image389.gif) ,可知
,可知试卷.files/image368.gif) 是等腰直角三角形,而
是等腰直角三角形,而试卷.files/image392.gif) 是斜边
是斜边试卷.files/image225.gif) 的中线。
的中线。
试卷.files/image395.gif) ①
①
同样由试卷.files/image221.gif) 底面
底面试卷.files/image398.gif) 得
得试卷.files/image400.gif)
试卷.files/image359.gif) 底面
底面试卷.files/image219.gif) 是正方形,有
是正方形,有试卷.files/image404.gif) 平面
平面试卷.files/image406.gif) 。
。
而试卷.files/image408.gif) 平面
平面试卷.files/image410.gif) ②
②
由①和②推得试卷.files/image412.gif) 平面
平面试卷.files/image414.gif)
而试卷.files/image408.gif) 平面
平面试卷.files/image417.gif)
又试卷.files/image227.gif) 且
且试卷.files/image420.gif) ,所以
,所以试卷.files/image239.gif) 平面
平面试卷.files/image241.gif)
(Ⅲ)解:由(Ⅱ)知,试卷.files/image424.gif) ,故
,故试卷.files/image426.gif) 是二面角
是二面角试卷.files/image243.gif) 的平面角
的平面角
由(2)知,试卷.files/image429.gif)
设正方形试卷.files/image219.gif) 的边长为
的边长为试卷.files/image255.gif) ,则
,则试卷.files/image433.gif)
试卷.files/image435.jpg)
试卷.files/image437.gif)
试卷.files/image439.gif)
在试卷.files/image441.gif) 中,
中,试卷.files/image443.gif)
在试卷.files/image445.gif) 中,
中,试卷.files/image447.gif)
试卷.files/image449.gif)
所以,二面角试卷.files/image243.gif) 的大小为
的大小为试卷.files/image452.gif)
方法二;如图所示建立空间直角坐标系,D为坐标原点,设试卷.files/image454.gif)
(I)证明:连结AC,AC交BD于G,连结EG。
依题意得A(试卷.files/image255.gif) ,0,0),P(0,0,
,0,0),P(0,0, 试卷.files/image255.gif) ),
),试卷.files/image457.gif)
试卷.files/image359.gif) 底面
底面试卷.files/image219.gif) 是正方形,
是正方形,试卷.files/image461.gif) 是此正方形的中心,故点
是此正方形的中心,故点试卷.files/image463.gif) 的坐标为
的坐标为试卷.files/image465.gif) )
)
且试卷.files/image467.gif) ,这表明
,这表明试卷.files/image469.gif)
而试卷.files/image471.gif) 平面
平面试卷.files/image375.gif) 且
且试卷.files/image377.gif) 平面
平面试卷.files/image475.gif) 平面
平面试卷.files/image375.gif)
(Ⅱ)证明:依题意得试卷.files/image478.gif) ,
,试卷.files/image480.gif)
又试卷.files/image482.gif) ,故
,故试卷.files/image484.gif)
由已知试卷.files/image227.gif) ,且
,且试卷.files/image487.gif) ,所以
,所以试卷.files/image239.gif) 平面
平面试卷.files/image241.gif)
(Ⅲ)解:设点试卷.files/image231.gif) 的坐标为
的坐标为试卷.files/image492.gif) ,则
,则试卷.files/image494.gif)
试卷.files/image496.gif) 则
则
试卷.files/image498.gif)
从而试卷.files/image500.gif) 所以
所以
试卷.files/image502.gif)
由条件试卷.files/image227.gif) 知,
知,试卷.files/image505.gif) ,即
,即
试卷.files/image507.gif) ,解得
,解得试卷.files/image509.gif)
试卷.files/image362.gif) 点
点试卷.files/image231.gif) 的坐标为
的坐标为试卷.files/image513.gif) ,且
,且试卷.files/image515.gif)
试卷.files/image517.gif)
即试卷.files/image519.gif) ,故
,故试卷.files/image426.gif) 二面角
二面角试卷.files/image243.gif) 的平面角。
的平面角。
试卷.files/image523.gif) ,且
,且
试卷.files/image525.gif)
试卷.files/image527.gif)
所以,二面角试卷.files/image243.gif) 的大小为
的大小为试卷.files/image452.gif) (或用法向量求)
(或用法向量求)
19.解:(I)设“从第一小组选出的2人均考《极坐标系与参数方程》”为事件A,“从第二小组选出的2人均考《极坐标系与参数方程》”为事件B,由于事件A、B相互独立,
且试卷.files/image531.gif)
所以选出的4人均考《极坐标系与参数方程》的概率为
试卷.files/image533.gif)
(Ⅱ)设试卷.files/image245.gif) 可能的取值为0,1,2,3,得
可能的取值为0,1,2,3,得
试卷.files/image536.gif)
试卷.files/image538.gif)
试卷.files/image245.gif) 的分布列为
的分布列为
试卷.files/image245.gif)
0
1
2
3
试卷.files/image300.gif)
试卷.files/image543.gif)
试卷.files/image545.gif)
试卷.files/image547.gif)
试卷.files/image549.gif)
试卷.files/image551.gif) 的数学期望
的数学期望试卷.files/image553.gif)
20.解:由题意试卷.files/image555.gif)
(I)当试卷.files/image557.gif) 时。
时。
由试卷.files/image559.gif) 得
得试卷.files/image561.gif) ,解得
,解得试卷.files/image563.gif) ,函数
,函数试卷.files/image200.gif) 的单调增区间是
的单调增区间是试卷.files/image566.gif) ;
;
由试卷.files/image568.gif) 得
得试卷.files/image570.gif) ,解得
,解得试卷.files/image572.gif) ,函数
,函数试卷.files/image200.gif) 的单调减区间是
的单调减区间是试卷.files/image575.gif)
试卷.files/image362.gif) 当
当试卷.files/image578.gif) 时,函数
时,函数试卷.files/image200.gif) 有极小值为
有极小值为试卷.files/image581.gif)
(2) 当试卷.files/image557.gif) 时,由于
时,由于试卷.files/image584.gif) ,均有
,均有试卷.files/image253.gif) ,
,
即试卷.files/image587.gif) 恒成立,
恒成立,
试卷.files/image589.gif) ,
,
由(I)知函数试卷.files/image200.gif) 极小值即为最小值,
极小值即为最小值,
试卷.files/image592.gif) ,解得
,解得试卷.files/image594.gif)
21.解(I)试卷.files/image359.gif) 方程
方程试卷.files/image259.gif) 有且只有一个根,
有且只有一个根,试卷.files/image598.gif) 或
或试卷.files/image600.gif)
又由题意知试卷.files/image602.gif) 舍去
舍去试卷.files/image604.gif)
当试卷.files/image606.gif) 时,
时,试卷.files/image608.gif)
当试卷.files/image610.gif) 时,
时,试卷.files/image612.gif) 也适合此等式
也适合此等式
试卷.files/image614.gif)
(Ⅱ)试卷.files/image616.gif)
试卷.files/image618.gif) ①
①
试卷.files/image620.gif) ②
②
由①-②得
试卷.files/image622.gif)
试卷.files/image624.gif)
(Ⅲ)法一:当试卷.files/image626.gif) 2时,
2时,试卷.files/image628.gif)
试卷.files/image630.gif) 时,数列
时,数列试卷.files/image632.gif) 单调递增,
单调递增,试卷.files/image634.gif)
又由(II)知试卷.files/image636.gif)
试卷.files/image638.gif)
法二:当试卷.files/image277.gif) 时,
时,试卷.files/image641.gif)
试卷.files/image643.gif)
试卷.files/image645.gif)
试卷.files/image647.gif)
22.(I)⊙M过点试卷.files/image649.gif) 三点,
三点,试卷.files/image362.gif) 圆心
圆心试卷.files/image292.gif) 既在
既在试卷.files/image653.gif) 的垂直平分线上,也在
的垂直平分线上,也在试卷.files/image655.gif) 的垂直平分线上,
的垂直平分线上,试卷.files/image653.gif) 的垂直平分线方程为
的垂直平分线方程为试卷.files/image658.gif)
试卷.files/image660.gif) 的中点为
的中点为试卷.files/image662.gif)
试卷.files/image664.gif) 的垂直平分线方程为
的垂直平分线方程为试卷.files/image666.gif)
由④⑤得试卷.files/image668.gif) 即
即试卷.files/image670.gif)
试卷.files/image672.gif) 在直线
在直线试卷.files/image296.gif) 上。
上。试卷.files/image675.gif)
试卷.files/image677.gif) 由
由试卷.files/image679.gif) 得
得试卷.files/image681.gif)
试卷.files/image362.gif) 椭圆的方程为
椭圆的方程为试卷.files/image684.gif)
(Ⅱ)设试卷.files/image686.gif) 则
则试卷.files/image688.gif)
试卷.files/image690.gif)
试卷.files/image692.gif) 是定值;
是定值;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com