
题目列表(包括答案和解析)
(1)在区间[-2,6]上画出函数f(x)的图象.
(2)设集合A={x|f(x)≥5},B=(-∞,-2]∪[0,4]∪[6,+∞).试判断集合A和B之间的关系,并给出证明.
(3)当k>2时,求证:在区间[-1,5]上,y=kx+3k的图象位于函数f(x)图象的上方.
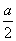 x2-1+cosx(a>0)。
x2-1+cosx(a>0)。 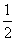 x2+ax+2lnx,a∈R,已知函数f(x)在x=1处有极值,
x2+ax+2lnx,a∈R,已知函数f(x)在x=1处有极值,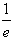 ,e](其中e是自然对数的底数)时,证明:e(e-x)(e+x-6)+4≥x4;
,e](其中e是自然对数的底数)时,证明:e(e-x)(e+x-6)+4≥x4;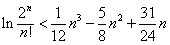 恒成立。
恒成立。| x2+a |
| bx-c |
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| an+1 |
| n+1 |
| n |
| 1 |
| an |
| 1 |
| m |
| 1 |
| m+1 |
| 1 |
| n |
| 2x-3 |
| x |
| y1-y2 |
| x2-x1 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com