练习册

  • 练习册
  • 试题
    2．方程:的曲线是什么图形? 教学设计说明 圆是学生比较熟悉的曲线.初中平面几何对圆的基本性质作了比较系统的研究.因此这节课的重点确定为用解析法研究圆的标准方程及其简单应用..首先.在已有圆的定义和求曲线方程的一般步骤的基础上.用实际问题引导学生探究获得圆的标准方程.然后.利用圆的标准方程由浅入深的解决问题,并通过圆的方程在实际问题中的应用.增强学生用数学的意识.另外.为了培养学生的理性思维.我分别在引例和问题四中.设计了两次由特殊到一般的学习思路.培养学生的归纳概括能力.在问题的设计中.我用一题多解的探究.纵向挖掘知识深度.横向加强知识间的联系.培养了学生的创新精神.并且使学生的有效思维量加大.随时对所学知识和方法产生有意注意.能力与知识的形成相伴而行.这样的设计不但突出了重点.更使难点的突破水到渠成. 本节课的设计了五个环节.以问题为纽带.以探究活动为载体.使学生在问题的指引下.教师的指导下把探究活动层层展开.步步深入.充分体现以教师为主导.以学生为主体的指导思想.应用启发式的教学方法把学生学习知识的过程转变为学生观察问题.发现问题.分析问题.解决问题的过程.在解决问题的同时锻炼了思维．提高了能力.培养了兴趣.增强了信心. 【查看更多】

     

    题目列表(包括答案和解析)

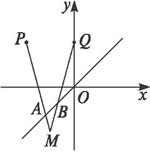
    已知两点P（-2，2）、Q（0，2），以及一条直线y=x，设长为的线段AB在直线上运动，如图，求直线PA和QB的交点M的轨迹方程，说明轨迹是什么曲线.

    查看答案和解析>>

    如图，已知点A（
    		3
    ，0），B（0，1），圆C是以AB为直径的圆，直线l：
    x=tcosφ
    y=-1+tsinφ
    ，（t为参数）．
    （1）以坐标原点为极点，x轴正半轴为极轴，建立极坐标系，求圆C的极坐标方程；
    （2）过原点O作直线l的垂线，垂足为H，若动点M0满足2
    OM
    =3
    OH
    ，当φ变化时，求点M轨迹的参数方程，并指出它是什么曲线．

    查看答案和解析>>

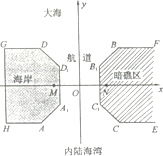    精英家教网某校兴趣小组运用计算机对轮船由海上行驶入内陆海湾进行了一次模拟试验．如图，内陆海湾的入口处有暗礁，图中阴影所示的区域为暗礁区，其中线段AA1，B1B，CC1，D1D关于坐标轴或原点对称，线段B1B的方程为y=x，x∈[a，b]，过o有一条航道．有一艘正在海面上航行的轮船准备进入内陆海湾，在点M(-
    		5
    2
    a，0)    处测得该船发出的汽笛声的时刻总晚1s（设海面上声速为am/s）．若该船沿着当前的航线航行（不考虑轮船的体积）
    （Ⅰ）问兴趣小组观察到轮船的当前的航线所在的曲线方程是什么？
    （Ⅱ）这艘船能否由海上安全驶入内陆海湾？请说明理由．

    查看答案和解析>>

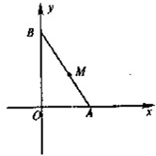    如图，在平面直角坐标系中，一条定长为m的线段其端点A、B分别在x轴、y轴上滑动，设点M满足
    AM
    =λ
    MB
    （λ是大于0的常数）．
    （Ⅰ）求点M的轨迹方程，并说明轨迹是什么曲线；
    （Ⅱ）若λ=2，已知直线l与原点O的距离为
    m
    2
    ，且直线l与动点M的轨迹有公共点，求直线l的斜率k的取值范围．

    查看答案和解析>>

    已知△OFQ的面积为2
    		6
    ，且
    OF
    •
    FQ
    =m    ．
    （1）设
    		6
    ＜m＜4
    		6
    ，求向量
    OF
    与
    FQ
    的夹角θ    正切值的取值范围；
    （2）设以O为中心，F为焦点的双曲线经过点Q（如图），|
    OF
    |=c，m=(
    		6
    4
    -1)c2    ，当|
    OQ
    |    取得最小值时，求此双曲线的方程．
    （3）设F1为（2）中所求双曲线的左焦点，若A、B分别为此双曲线渐近线l1、l2上的动点，且2|AB|=5|F1F|，求线段AB的中点M的轨迹方程，并说明轨迹是什么曲线．

    查看答案和解析>>


    同步练习册答案