
题目列表(包括答案和解析)
对于以下结论:
①.对于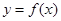 是奇函数,则
是奇函数,则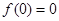 ;
;
②.已知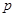 :事件
:事件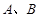 是对立事件;
是对立事件;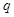 :事件
:事件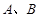 是互斥事件;则
是互斥事件;则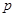 是
是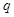 的必要但不充分条件;
的必要但不充分条件;
③.若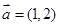 ,
,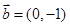 ,则
,则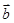 在
在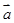 上的投影为
上的投影为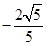 ;
;
④.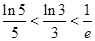 (
(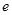 为自然对数的底);
为自然对数的底);
⑤.函数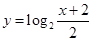 的图像可以由函数
的图像可以由函数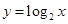 图像先左移2个单位,再向下平移1个单位而来.
图像先左移2个单位,再向下平移1个单位而来.
其中,正确结论的序号为__________________.
对于以下结论:
①.对于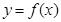 是奇函数,则
是奇函数,则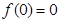 ;
;
②.已知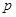 :事件
:事件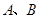 是对立事件;
是对立事件;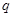 :事件
:事件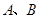 是互斥事件;则
是互斥事件;则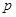 是
是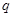 的必要但不充分条件;
的必要但不充分条件;
③.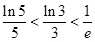 (
(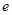 为自然对数的底);
为自然对数的底);
④.若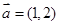 ,
,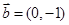 ,则
,则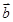 在
在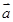 上的投影为
上的投影为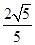 ;
;
⑤.若随机变量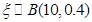 ,则
,则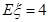 .
.
其中,正确结论的序号为___________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com