
题目列表(包括答案和解析)
(04年上海卷)(16分)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点, 截面DEF∥底面ABC, 且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
(1) 证明:P-ABC为正四面体;
(2) 若PD=![]() PA, 求二面角D-BC-A的大小;(结果用反三角函数值表示)
PA, 求二面角D-BC-A的大小;(结果用反三角函数值表示)
(3) 设棱台DEF-ABC的体积为V, 是否存在体积为V且各棱长均相等的直
平行六面体,使得它与棱台DEF-ABC有相同的棱长和? 若存在,请具体构造
出这样的一个直平行六面体,并给出证明;若不存在,请说明理由.

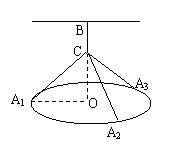
(本小题满分16分)如图所示:一吊灯的下圆环直径为4m,圆心为O,通过细绳悬挂在天花板上,圆环呈水平状态,并且与天花板的距离![]() 为2m,在圆环上设置三个等分点A1,A2,A3.点C为
为2m,在圆环上设置三个等分点A1,A2,A3.点C为![]() 上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等.设细绳的总长为ym.
上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等.设细绳的总长为ym.
(1)①设∠CA1O = ![]() (rad),将y表示成θ的函数关系式;
(rad),将y表示成θ的函数关系式;
②设CO=x m, 将y表示成x的函数关系式;
 (2)请你选用(1)中的一个函数关系确定BC的长使细绳总长y 最小.
(2)请你选用(1)中的一个函数关系确定BC的长使细绳总长y 最小.
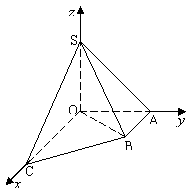 (本题满分16分)如图直角梯形OABC中,∠COA=∠OAB=
(本题满分16分)如图直角梯形OABC中,∠COA=∠OAB=![]() ,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
⑴求![]() 的大小(用反三角函数表示);
的大小(用反三角函数表示);
⑵设![]()
①![]() ②OA与平面SBC的夹角
②OA与平面SBC的夹角![]() (用反三角函数表示);
(用反三角函数表示);
③O到平面SBC的距离.
⑶设![]()
①![]() . ②异面直线SC、OB的距离为 .(注:⑶只要求写出答案)
. ②异面直线SC、OB的距离为 .(注:⑶只要求写出答案)
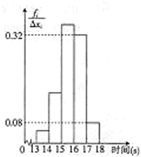 (2012•安徽模拟)为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.
(2012•安徽模拟)为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.(本小题满分16分)已知函数 的图象在
的图象在 上连续不断,定义:
上连续不断,定义:
 ,
,
其中, 表示函数
表示函数 在区间上的最小值,
在区间上的最小值, 表示函数
表示函数 在区间上的最大值.若存在最小正整数
在区间上的最大值.若存在最小正整数 ,使得
,使得 对任意的
对任意的 成立,则称函数为区间
成立,则称函数为区间 上的“
上的“ 阶收缩函数”.
阶收缩函数”.
(1)若 ,试写出
,试写出 的表达式;
的表达式;
(2)已知函数 试判断
试判断 是否为
是否为 上的“
上的“ 阶收缩函数”,如果是,求出相应的
阶收缩函数”,如果是,求出相应的 ;如果不是,请说明理由;
;如果不是,请说明理由;
(3)已知 函数
函数 是
是 上的2阶收缩函数,求
上的2阶收缩函数,求 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com