
题目列表(包括答案和解析)
要测量河对岸的烟囱AB的高,而测量者不能到达它的底部,如何解决这一问题?
数学离不开算法,中国古代算法是数学发展史上一颗璀璨的明珠,而许多算法趣题更在世界上广泛流传,例如:百钱买百鸡,鸡兔同笼问题,韩信点兵不知其数等,你能找出它们各是什么问题,如何解决吗?你还能找到更多的算法故事吗?和你的好朋友们互相交流.
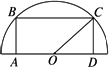
材料:为了美化环境,某房地产公司打算在所管辖的一个居民小区内的一块半圆形空地上,划出一个内接矩形辟为绿地,且使矩形的一边落在半圆的直径上,而另外两个顶点在半圆的圆周上,已知半圆的半径为30米.为了使绿地的面积最大,该公司请了本公司的一位设计师,设计出了这个半圆内接矩形的长与宽的关系.该设计师的计算过程如下:
如下图,设CD=x,则OD=![]() ,矩形的面积设为S,则
,矩形的面积设为S,则
S=2x·![]() =
=![]() .
.
所以当x2=450,即x=![]() 时,S有最大值,即此时矩形的面积最大.
时,S有最大值,即此时矩形的面积最大.
问题:现在我们已经学习了三角函数的有关知识,利用三角函数的知识该如何解决这一问题?
1.如下图所示,点光源S发出光线经平面镜M反射后,恰好经过P点,试求其入射点.
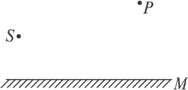
2.那么上题该如何解决呢?
你以前听说过“鸡兔同笼”问题吗?这个问题,是我国古代著名趣题之一.大约在1 500年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚.求笼中各有几只鸡和兔?
你会解答这个问题吗?你想知道《孙子算经》中是如何解答这个问题的吗?
解答思路是这样的:假如砍去每只鸡、每只兔一半的脚,则每只鸡就变成了“独角鸡”,每只兔就变成了“双脚兔”.这样,(1)鸡和兔的脚的总数就由94只变成了47只;(2)如果笼子里有一只兔子,则脚的总数就比头的总数多1.因此,脚的总只数47与总头数35的差,就是兔子的只数,即47-35=12(只).显然,鸡的只数就是35-12=23(只)了.
这一思路新颖而奇特,其“砍足法”也令古今中外数学家赞叹不已.这种思维方法叫化归法.
化归法就是在解决问题时,先不对问题采取直接的分析,而是将题中的条件或问题进行变形,使之转化,直到最终把它归成某个已经解决的问题.
1.古代《孙子算经》就有这么好的解法——化归法,这一思路新颖而奇特,其“砍足法”也令古今中外数学家赞叹不已.对此,谈谈你的看法.
2.我国古代数学研究一直处于领先地位,现在有所落后了,对此,我们不应只感叹古人的伟大,而更应该树立为科学而奋斗终身的信心,同学们,你们准备好了吗?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com