
题目列表(包括答案和解析)
 某中学,由于不断深化教育改革,办学质量逐年提高.2006年至2009年高考考入一流大学人数如下:
某中学,由于不断深化教育改革,办学质量逐年提高.2006年至2009年高考考入一流大学人数如下:| 年 份 | 2006 | 2007 | 2008 | 2009 |
| 高考上线人数 | 116 | 172 | 220 | 260 |
| 年 份 | 2006 | 2007 | 2008 | 2009 |
| 年份代码x | 1 | 2 | 3 | 4 |
| 实际上线人数 | 116 | 172 | 220 | 260 |
| 模拟上线人数 | y1=a+b | y2=2a+b | y3=3a+b | y4=4a+b |
(14分)2006年5月3日进行抚仙湖水下考古,潜水员身背氧气瓶潜入湖底进行
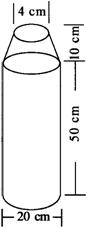
考察,氧气瓶形状如图,其结构为一个圆柱和一个圆台的组合(设氧气瓶中氧气已充满,所
给尺寸是氧气瓶的内径尺寸),潜水员在潜入水下 米的过程中,速度为
米的过程中,速度为 米/分,每分钟
米/分,每分钟
需氧量与速度平方成正比(当速度为1米/分时,每分钟需氧量为0.2L);在湖底工作时,
每分钟需氧量为0.4 L;返回水面时,速度也为 米/分,每分钟需氧量为0.2 L,若下
米/分,每分钟需氧量为0.2 L,若下
潜与上浮时速度不能超过p米/分,试问潜水员在湖底最多能工作多少时间?(氧气瓶体积
计算精确到1 L, 、p为常数,圆台的体积V=
、p为常数,圆台的体积V= ,其中h为高,r、R分
,其中h为高,r、R分
别为上、下底面半径.)
深化教育改革,办学质量逐年提高。2006年至2009年高考考入一流大学人数如下:
| 年 份 | 2006 | 2007 | 2008 | 2009 |
| 高考上线人数 | 116 | 172 | 220 | 260 |
以年份为横坐标,当年高考上线人数为纵坐标建立直角坐标系,由所给数据描点作图(如图所示),从图中可清楚地看到这些点基本上分布在一条直线附近,因此,用一次函数![]() 来模拟高考上线人数与年份的函数关系,并以此来预测2010年高考一本上线人数.如下表:
来模拟高考上线人数与年份的函数关系,并以此来预测2010年高考一本上线人数.如下表:
| 年 份 | 2006 | 2007 | 2008 | 2009 |
| 年份代码 | 1 | 2 | 3 | 4 |
| 实际上线人数 | 116 | 172 | 220 | 260 |
| 模拟上线人数 |
|
|
|
|
为使模拟更逼近原始数据,用下列方法来确定模拟函数。
设![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 表示各年实际上线人数,
表示各年实际上线人数,![]() 、
、![]() 、
、![]() 、
、![]() 表示模拟上线人数,当
表示模拟上线人数,当![]() 最小时,模拟函数最为理想。试根据所给数据,预测2010年高考上线人数。
最小时,模拟函数最为理想。试根据所给数据,预测2010年高考上线人数。
(2006年广东卷)设函数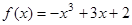 分别在
分别在 、
、 处取得极小值、极大值.
处取得极小值、极大值. 平面上点A、B的坐标分别为
平面上点A、B的坐标分别为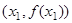 、
、 ,该平面上动点P满足
,该平面上动点P满足 ,点Q是点P关于直线
,点Q是点P关于直线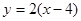 的对称点
的对称点
求:(Ⅰ)点A、B的坐标 ;
(Ⅱ)动点Q的轨迹方程
(2006年安徽卷)已知函数 在R上有定义,对任何实数
在R上有定义,对任何实数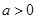 和任何实数
和任何实数 ,都有
,都有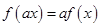
(Ⅰ)证明 ;
;
(Ⅱ)证明 其中
其中 和
和 均为常数;
均为常数;
(Ⅲ)当(Ⅱ)中的 时,设
时,设 ,讨论
,讨论 在
在 内的单调性并求极值.
内的单调性并求极值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com