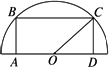
材料：为了美化环境，某房地产公司打算在所管辖的一个居民小区内的一块半圆形空地上，划出一个内接矩形辟为绿地，且使矩形的一边落在半圆的直径上，而另外两个顶点在半圆的圆周上，已知半圆的半径为30米．为了使绿地的面积最大，该公司请了本公司的一位设计师，设计出了这个半圆内接矩形的长与宽的关系．该设计师的计算过程如下：

如下图，设CD＝x，则OD＝，矩形的面积设为S，则

S＝2x·＝．

所以当x²＝450，即x＝时，S有最大值，即此时矩形的面积最大．

问题：现在我们已经学习了三角函数的有关知识，利用三角函数的知识该如何解决这一问题？