
题目列表(包括答案和解析)
在 平面上,将两个半圆弧
平面上,将两个半圆弧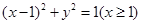 和
和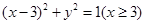 、两条直线
、两条直线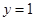 和
和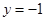 围成的封闭图形记为D,如图中阴影部分.记D绕y轴旋转一周而成的几何体为
围成的封闭图形记为D,如图中阴影部分.记D绕y轴旋转一周而成的几何体为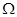 ,过
,过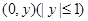 作
作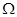 的水平截面,所得截面面积为
的水平截面,所得截面面积为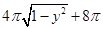 ,试利用祖暅原理、一个平放的圆柱和一个长方体,得出
,试利用祖暅原理、一个平放的圆柱和一个长方体,得出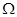 的体积值为__________
的体积值为__________
我国齐梁时代的数学家祖暅(公元前5-6世纪)提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任何平面所截,如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等.
设:由曲线 和直线
和直线 ,
, 所围成的平面图形,绕
所围成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为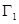 ;由同时满足
;由同时满足 ,
, ,
, ,
, 的点
的点 构成的平面图形,绕
构成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 .根据祖暅原理等知识,通过考察
.根据祖暅原理等知识,通过考察 可以得到
可以得到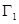 的体积为
的体积为
A. B.
B. C.
C. D.
D.
我国齐梁时代的数学家祖暅(公元5-6世纪)提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任何平面所截,如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等.
设:由曲线 和直线
和直线 ,
, 所围成的平面图形,绕
所围成的平面图形,绕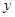 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 ;由同时满足
;由同时满足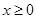 ,
, ,
, ,
, 的点
的点 构成的平面图形,绕
构成的平面图形,绕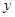 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 .根据祖暅原理等知识,通过考察
.根据祖暅原理等知识,通过考察 可以得到
可以得到 的体积为
的体积为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com