
题目列表(包括答案和解析)
(本题14分)
某公司将进货单价为8元一个的商品按10元一个销售,每天可以卖出100个,若这种商品的销售价每个上涨一元,则销售量就减少8个.
(1)求销售价为13元时每天的销售利润;
(2)如果销售利润为336元,那么销售价上涨了几元?
(3)设销售价上涨x元( )试将利润y表示为x的函数,并求出上涨几元,可获最大利润.
)试将利润y表示为x的函数,并求出上涨几元,可获最大利润.
(本题满分14分)
某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视
观众,相关的数据如下表所示:
|
|
文艺节目 |
新闻节目 |
总计 |
|
20至40岁 |
40 |
18 |
58 |
|
大于40岁 |
15 |
27 |
42 |
|
总计 |
55 |
45 |
100 |
(1) 由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(2) 用分层抽样方法在收看新闻节目的观众中随机抽出5名,大于40岁的观众应该
抽取几名?
(3) 在上述抽取的5名观众中任取出2名,求恰有1名观众年龄20岁至40岁的概率。
((本题14分)定义:若函数 在某一区间D上任取两个实数
在某一区间D上任取两个实数 、
、 ,且
,且 ,都有
,都有 ,则称函数
,则称函数 在区间D上具有性质L。
在区间D上具有性质L。
(1)写出一个在其定义域上具有性质L的对数函数(不要求证明)。
(2)对于函数 ,判断其在区间
,判断其在区间 上是否具有性质L?并用所给定义证明你的结论。
上是否具有性质L?并用所给定义证明你的结论。
(3)若函数 在区间(0,1)上具有性质L,求实数
在区间(0,1)上具有性质L,求实数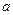 的取值范围。
的取值范围。
((本题满分14分)某射手每次射击击中目标的概率是,且各次射击的结果互不影响。
(1)假设这名射手射击5次,求恰有2次击中目标的概率;
(2)假设这名射手射击5次,求有3次连续击中目标,另外2次未击中目标的概率;
(3)假设这名射手射击3次,每次射击,击中目标得1分,未击中目标得0分.在3次射击中,若有2次连续击中,而另外1次未击中,则额外加1分;若3次全击中,则额外加3分.记ξ为射手射击3次后的总得分数,求ξ的分布列.
(本题14分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)
与相应的生产能耗y(吨标准煤)的几组对照数据
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(1) 请根据上表提供的数据,求出y关于x的线性回归方程![]() ;
;
(2) 已知该厂技术改造前100吨甲产品能耗为90吨标准煤. 请进行线性相关性分析,如果有95﹪以上把握说具有线性相关性,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考数据: 3×2.5+4×3+5×4+6×4.5=66.5)
| n-2 | 0.05 | 0.01 |
| 2 | 0.950 | 0.990 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com