
题目列表(包括答案和解析)
(2011年福建质检)为了解某地居民的月收入情况,一个社会调查机构调查了20000人,并根据所得数据画出样本的频率分布直方图如图.现按月收入分层,用分层抽样的方法在这20000人中抽出200人作进一步调查,则月收入在[1500,2000)(单位:元)的应抽取________人.

(08年福建师大附中模拟)(12分)
某车间某两天内,每天都生产![]() 件产品,其中第一天生产了1件次品,第二天生产了2件次品,质检部每天要从生产的
件产品,其中第一天生产了1件次品,第二天生产了2件次品,质检部每天要从生产的![]() 件产品中随意抽取4件进行检查,若发现有次品,则当天的产品不能通过。已知第一天通过检查的概率为
件产品中随意抽取4件进行检查,若发现有次品,则当天的产品不能通过。已知第一天通过检查的概率为![]()
(1)求![]() 的值
的值
(2)求两天都通过检查的概率
(3)求两天中至少有一天通过检查的概率
(04年福建卷)(12分)
某企业2003年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降。若不能进行技术改造,预测从今年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年)的利润为500(1+![]() )万元(n为正整数)。
)万元(n为正整数)。
(Ⅰ)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为An万元,进行技术改造后的累计纯利润为Bn万元(须扣除技术改造资金),求An、Bn的表达式;
(Ⅱ)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
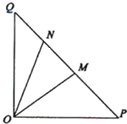 (2013•福建)如图,在等腰直角△OPQ中,∠POQ=90°,OP=2
(2013•福建)如图,在等腰直角△OPQ中,∠POQ=90°,OP=2| 2 |
| 5 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com