
题目列表(包括答案和解析)
在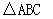 中,内角A,B,C所对的分别是a,b,c。已知a=2,c=
中,内角A,B,C所对的分别是a,b,c。已知a=2,c=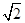 ,cosA=
,cosA= .
.
(I)求sinC和b的值;
(II)求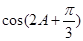 的值。
的值。
【考点定位】本小题主要考查同角三角函数的基本关系、二倍角的正弦与余弦公式、两角和余弦公式以及正弦定理、余弦定理等基础知识,考查基本运算求解能力.
已知△ 的内角
的内角 所对的边分别为
所对的边分别为 且
且 .
.
(1)
若 , 求
, 求 的值;
的值;
(2)
若△ 的面积
的面积 求
求 的值.
的值.
【解析】本小题主要考查正弦定理、余弦定理、同角三角函数的基本关系等基础知识,考查运算求解能力。第一问中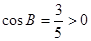 ,得到正弦值
,得到正弦值 ,再结合正弦定理可知,
,再结合正弦定理可知, ,得到
,得到 (2)中
(2)中 即
即 所以c=5,再利用余弦定理
所以c=5,再利用余弦定理 ,得到b的值。
,得到b的值。
解: (1)∵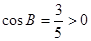 , 且
, 且 , ∴
, ∴  . 由正弦定理得
. 由正弦定理得 , ∴
, ∴ .
.
(2)∵ ∴
∴ . ∴c=5
. ∴c=5
由余弦定理得 ,
,
∴ 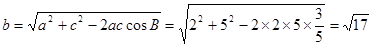
同角三角函数的基本关系公式主要有哪些方面的用途,谈谈你的体会.
从本节的例
7可以看出,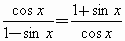 就是
就是 的一个变形.你能利用同角三角函数的基本关系推导出更多的关系式吗?
的一个变形.你能利用同角三角函数的基本关系推导出更多的关系式吗?湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com