练习册

  • 练习册
  • 试题
    处理方法:引入辅助角 .化为y=sin(x+),利用函数即可求解.Y=asinx+bsinxcosx+mcosx+n型亦可以化为此类. 例3 .已知f(x)=2cosx+sin2x+a,若x＜2,求a的取值范围. 注:本题综合运用三角恒等变形.三角函数的单调性.不等式的性质.函数的恒成立等知识.是一个较好的三角函数综合题. 例4．求函数y=a sin x + b cos x的最值. 解:y=a sin x + b cos x=sin(x + arc tg) ∴当x=2k+--arc tg时.ymax = 当x=2k+--arc tg时.ymin =-- 例5．求函数y= sin2x+2sinx cosx+3 cos2x的最小值.最大值.并写出函数y 取 最值时的x的集合. 解:∵y= sin 2x + 2cos2x + 1 = sin 2x + cos 2x + 2 = sin(2x +)+ 2 ∴当sin(2x +)= --1时. 有ymin = 2 --. 当sin(2x +)= 1时.有ymax = 2 +. 此时有2x + = 2k--, x = k-- (kz) 2x + = 2k + , x = k+ (kz) 故函数y取最小值2--时x 的集合是{x∣x = k--, kz } y取最大值2 +时x 的集合是{x∣x = k+, kz } 从上面三例可以清晰地看出.这一类的三角函数的最值求解中运用的基本的方法是“利用辅助角法 .将较复杂的三角式转化成“Asin() 的形式.将异名三角比化归成同名三角比.同时.也应对自变量的取值范围要仔细地考察. 【查看更多】

     

    题目列表(包括答案和解析)

    把asinθ+bcosθ（ab≠0）化成
    		a2+b2
    sin(θ+φ)    时，以下关于辅助角φ的表述中，不正确的是（　　）

    查看答案和解析>>

    阅读下面材料：根据两角和与差的正弦公式，有
    sin（α+β）=sinαcosβ+cosαsinβ------①
    sin（α-β）=sinαcosβ-cosαsinβ------②
    由①+②得sin（α+β）+sin（α-β）=2sinαcosβ------③
    令α+β=A，α-β=β 有α=
    A+B
    2
    ，β=
    A-B
    2

    代入③得 sinA+subB=2sin
    A+B
    2
    cos
    A-B
    2
    ．
    （Ⅰ） 类比上述推理方法，根据两角和与差的余弦公式，证明：cosA-cosB=-2sin
    A+B
    2
    sin
    A-B
    2
    ；
    （Ⅱ）求值：sin220°+cos250°+sin20°cos50°（提示：如果需要，也可以直接利用阅读材料及（Ⅰ）中的结论）

    查看答案和解析>>

    （2012•福建模拟）阅读下面材料：
    根据两角和与差的正弦公式，有sin（α+β）=sinαcosβ+cosαsinβ------①
    sin（α-β）=sinαcosβ-cosαsinβ------②
    由①+②得sin（α+β）+sin（α-β）=2sinαcosβ------③
    令α+β=A，α-β=B有α=
    A+B
    2
    ，β=
    A-B
    2

    代入③得 sinA+sinB=2sin
    A+B
    2
    cos
    A-B
    2
    ．
    （Ⅰ）类比上述推证方法，根据两角和与差的余弦公式，证明：cosA-cosB=-2sin
    A+B
    2
    sin
    A-B
    2
    ；
    （Ⅱ）若△ABC的三个内角A，B，C满足cos2A-cos2B=2sin2C，试判断△ABC的形状．
    （提示：如果需要，也可以直接利用阅读材料及（Ⅰ）中的结论）

    查看答案和解析>>

    由“若直角三角形两直角边的长分别为a，b，将其补成一个矩形，则根据矩形的对角线长可求得该直角三角形外接圆的半径为r=
    		a2+b2
    2
    ”．对于“若三棱锥三条侧棱两两垂直，侧棱长分别为a，b，c”，类比上述处理方法，可得该三棱锥的外接球半径为R=
     
    ．

    查看答案和解析>>

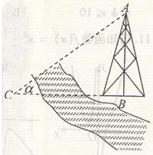    精英家教网如图，测量河对岸的塔形建筑AB，A为塔的顶端，B为塔的底端，河两岸的地面上任意一点与塔底端B处在同一海拔水平面上，现给你一架测角仪（可以测量仰角、俯角和视角），再给你一把尺子（可以测量地面上两点问距离），图中给出的是在一侧河岸地面C点测得仰角∠ACB=α，请设计一种测量塔形建筑高度AB的方法（其中测角仪支架高度忽略不计，计算结果可用测量数据所设字母表示）．

    查看答案和解析>>


    同步练习册答案