练习册

  • 练习册
  • 试题
    理.20)在直角坐标系xOy中,椭圆C1: =1 的左.右焦点分别为F1.F2.F2也是抛物线C2:y2=4x的焦点.点M为C1与C2在第一象限的交点.且|MF2|=. (1)求C1的方程, (2)平面上的点N满足=+.直线l∥MN.且与C1交于A.B两点.若·=0.求直线l的方程. 解 (1)由C2:y2=4x,知F2(1,0), 设M(x1,y1),M在C2上, 因为|MF2|=,所以x1+1=, 得x1=,y1=.所以M. M在C1上,且椭圆C1的半焦距c=1, 于是 消去b2并整理得9a4-37a2+4=0. 解得a=2(a=不合题意,舍去). 故b2=4-1=3. 故椭圆C1的方程为. (2)由=+,知四边形MF1NF2是平行四边形,其中心为坐标原点O, 因为l∥MN,所以l与OM的斜率相同. 故l的斜率k==. 设l的方程为y=(x-m). 由消去y并整理得 9x2-16mx+8m2-4=0. 设A(x1,y1),B(x2,y2), 则x1+x2=,x1x2=. 因为⊥,所以x1x2+y1y2=0. 所以x1x2+y1y2=x1x2+6(x1-m)(x2-m) =7x1x2-6m(x1+x2)+6m2 =7·-6m·+6m2 =(14m2-28)=0. 所以m=±.此时Δ=(16m)2-4×9(8m2-4)＞0. 故所求直线l的方程为y=x-2,或y=x+2. 【查看更多】

     

    题目列表(包括答案和解析)

    (2008海南、宁夏高考,理13)已知向量＝(0,-1,1), ＝(4,1,0),|λ+|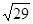＝,且λ＞0,则λ＝________________.

     

    查看答案和解析>>

    （2008海南、宁夏）（    ）   

    A．       B．     C．       D．

    查看答案和解析>>

    19、在2008年北京奥运会羽毛球女单决赛中，中国运动员张宁以2：1力克排名世界第一的队友谢杏芳，蝉联奥运会女单冠军．羽毛球比赛按“三局二胜制”的规则进行（即先胜两局的选手获胜，比赛结束），且各局之间互不影响．根据两人以往的交战成绩分析，谢杏芳在前两局的比赛中每局获胜的概率是0.6，但张宁在前二局成1：1的情况下，在第三局中凭借过硬的心理素质，获胜的概率为0.6．若张宁与谢杏芳下次在比赛上相遇．
    （1）求张宁以2：1获胜的概率；
    （2）设张宁的净胜局数为ξ，求ξ的分布列及Eξ．

    查看答案和解析>>

    在2008年北京奥运会羽毛球女单决赛中，中国运动员张宁以2：1力克排名世界第一的队友谢杏芳，蝉联奥运会女单冠军.羽毛球比赛按“三局二胜制”的规则进行（即先胜两局的选手获胜，比赛结束），且各局之间互不影响.根据两人以往的交战成绩分析，谢杏芳在前两局的比赛中每局获胜的概率是0.6，但张宁在前二局战成1：1的情况下，在第三局中凭借过硬的心理素质，获胜的概率为0.6.若张宁与谢杏芳下次在比赛上相遇.

    （1）求张宁以2：1获胜的概率；

    （2）求张宁失利的概率. （12分）

     

    查看答案和解析>>

    在2008年北京奥运会羽毛球女单决赛中，中国运动员张宁以2∶1力克队友谢杏芳，蝉联奥运会女单冠军.羽毛球比赛按“三局两胜制”的规则进行(即先胜两局的选手获胜，比三结束)，且各局之间互不影响.根据两人以往的交战成绩分析，谢杏芳在前两局的比赛中每局获胜的概率是0.6，但张宁在前两局战成1∶1的情况下，在第三局中凭借过硬的心理素质，获胜的概率为0.6，若张宁与谢杏芳在下次比赛中相遇.

    (1)求张宁以2∶1获胜的概率；

    (2)设张宁的净胜局数为ξ，求ξ的分布列及Eξ.

    查看答案和解析>>


    同步练习册答案