
题目列表(包括答案和解析)
对于定义域为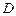 的函数
的函数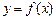 ,若有常数M,使得对任意的
,若有常数M,使得对任意的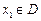 ,存在唯一的
,存在唯一的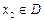 满足等式
满足等式 ,则称M为函数
,则称M为函数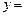 f (x)的“均值”.
f (x)的“均值”.
(1)判断1是否为函数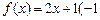 ≤
≤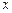 ≤
≤ 的“均值”,请说明理由;
的“均值”,请说明理由;
(2)若函数
 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围;
(3)若函数 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数 的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
说明:对于(3),将根据结论的完整性与一般性程度给予不同的评分
对于定义域为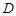 的函数
的函数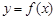 ,若有常数M,使得对任意的
,若有常数M,使得对任意的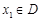 ,存在唯一的
,存在唯一的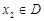 满足等式
满足等式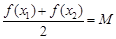 ,则称M为函数
,则称M为函数 f (x)的“均值”.
f (x)的“均值”.
(1)判断1是否为函数 ≤
≤ ≤
≤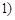 的“均值”,请说明理由;
的“均值”,请说明理由;
(2)若函数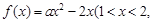
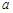 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围;
(3)若函数 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数 的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
说明:对于(3),将根据结论的完整性与一般性程度给予不同的评分
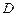 的函数
的函数 ,若有常数M,使得对任意的
,若有常数M,使得对任意的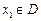 ,存在唯一的
,存在唯一的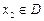 满足等式
满足等式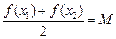 ,则称M为函数
,则称M为函数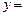 f (x)的“均值”.
f (x)的“均值”.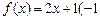 ≤
≤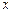 ≤
≤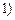 的“均值”,请说明理由;
的“均值”,请说明理由;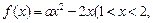
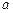 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围; 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数 的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).求下列幂函数的定义域,并指出其奇偶性、单调性.
(1)y=![]() ;(2)y=
;(2)y=![]() ;(3)y=
;(3)y=![]() ;(4)y=x-2.
;(4)y=x-2.
问题1:观察以上函数的解析式,你能发现解析式中对于自变量x都有哪些限制条件吗?
问题2:如何来判断函数的奇偶性呢?
3.探究:请同学们根据我们以上的分析,把上述函数图象的大概形状画出来.并总结归纳幂函数的指数变化时对幂函数定义域的影响.
若函数![]() 满足下列条件:在定义域内存在
满足下列条件:在定义域内存在![]() 使得
使得![]() 成立,则称函数
成立,则称函数![]() 具有性质
具有性质![]() ;反之,若
;反之,若![]() 不存在,则称函数
不存在,则称函数![]() 不具有性质
不具有性质![]() .
.
(1)证明:函数![]() 具有性质
具有性质![]() ,并求出对应的
,并求出对应的![]() 的值;
的值;
(2)已知函数![]() 具有性质
具有性质![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)试探究形如①![]() 、②
、②![]() 、③
、③![]() 、④
、④![]() 、⑤
、⑤![]() 的函数,指出哪些函数一定具有性质
的函数,指出哪些函数一定具有性质![]() ?并加以证明.
?并加以证明.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com