
题目列表(包括答案和解析)
(本小题满分12分) 海水受日月的引力,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天从0时至24时的时间![]() (单位:时)与水深y(单位:米)的关系表:
(单位:时)与水深y(单位:米)的关系表:
|
| 0:00 | 3:00 | 6:00 | 9: 00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
|
| 12.0 | 15.0 | 12.0 | 9.0 | 12.0 | 15.0 | 12.0 | 9.0 | 12.0 |
(1)请选用一个函数来近似描述这个港口的水深与时间的函数关系;
(2)一条货轮的吃水深度(船体最低点与水面的距离)为12米,安全条例规定船体最低点与
洋底间隙至少要有1.5米,请问该船何时能进出港口?在港口最多能停留多长时间?
| 3 | 4 |
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8分,第3小题满分6分.
已知负数 和正数
和正数 ,且对任意的正整数n,当
,且对任意的正整数n,当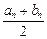 ≥0时, 有[
≥0时, 有[ ,
,  ]=
]=
[ ,
, 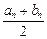 ];当
];当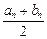 <0时, 有[
<0时, 有[ ,
,  ]= [
]= [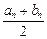 ,
, 
 ].
].
(1)求证数列{ }是等比数列;
}是等比数列;
(2)若 ,求证
,求证
 ;
;
(3)是否存在 ,使得数列
,使得数列 为常数数列?请说明理由
为常数数列?请说明理由
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
在平行四边形 中,已知过点
中,已知过点 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若 。
。
(1)求证: 与
与 的关系为
的关系为 ;
;
(2)设 ,定义函数
,定义函数 ,点列
,点列 在函数
在函数 的图像上,且数列
的图像上,且数列 是以首项为1,公比为
是以首项为1,公比为 的等比数列,
的等比数列, 为原点,令
为原点,令 ,是否存在点
,是否存在点
 ,使得
,使得 ?若存在,请求出
?若存在,请求出 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。
(3)设函数 为
为 上偶函数,当
上偶函数,当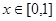 时
时 ,又函数
,又函数 图象关于直线
图象关于直线 对称, 当方程
对称, 当方程 在
在 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数 的取值范围。
的取值范围。
(本题满分18分,第1小题6分,第2小题6分,第3小题6分)
对于定义在D上的函数 ,若同时满足
,若同时满足
(Ⅰ)存在闭区间 ,使得任取
,使得任取 ,都有
,都有 是常数);
是常数);
(Ⅱ)对于D内任意 ,当
,当 时总有
时总有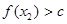 ,则称
,则称 为“平底型”函数。
为“平底型”函数。
(1)判断 是否是“平底型”函数?简要说明理由;
是否是“平底型”函数?简要说明理由;
(2)设 是(1)中的“平底型”函数,若
是(1)中的“平底型”函数,若 ,对一切
,对一切 恒成立,求实数
恒成立,求实数 的范围;
的范围;
(3)若 是“平底型”函数,求
是“平底型”函数,求 和
和 满足的条件,并说明理由。
满足的条件,并说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com