题目列表(包括答案和解析)
（本小题满分12分）
已知函数
；
（1）求
; （2）求
的最大值与最小值.
【解析】第一问利用导数的运算法则，幂函数的导数公式，可得。
第二问中，利用第一问的导数，令导数为零，得到
然后结合导数，函数的关系判定函数的单调性，求解最值即可。
导数的运算法则
[f(x)±g(x)
＝_________；
[f(x)·g(x)＝_________；
[
＝_________(g(x)≠0)．
已知偶函数y＝f(x)＝ax2＋bx＋c的最小值为－1，且f(1)＝0．
(1)求该函数的表达式f(x)．
(2)过曲线C：y＝f(x)(x＞0)上的点P作曲线C的切线，与x轴、y轴分别交于点M，N，试确定点P的坐标，使△MON的面积最小．
[求商的导数的法则是：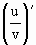
＝
]
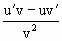函数的和、差、积、商的求导法则
(1)法则1：两个函数的和(或差)的导数，等于这两个函数的导数的和(或差)，即：_________．
(2)法则2：两个函数的积的导数，等于第一个函数的导数乘以第二个函数加上第一个函数乘以第二个函数的导数，即：_________．
(3)常数与函数的积的导数等于常数乘以函数的导数，即：_________．
(4)法则3：两个函数的商的导数，等于分子的导数与分母的积，减去分母的导数与分子的积，再除以分母的平方，即：_________．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com