
题目列表(包括答案和解析)
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| AB |
| a |
| b |
| AC |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| 13 |
| a |
| b |
给出以下四个命题:
①对任意两个向量a,b都有|a·b|=|a||b|;
②若a,b是两个不共线的向量,且![]() =λ1a+b,
=λ1a+b,![]() =a+λ2b(λ1,λ2∈R),则A、B、C共线⇔λ1λ2=-1;
=a+λ2b(λ1,λ2∈R),则A、B、C共线⇔λ1λ2=-1;
③若向量a=(cosα,sinα),b=(cosβ,sinβ),则a+b与a-b的夹角为90°.
④若向量a、b满足|a|=3,|b|=4,|a+b|=![]() ,则a,b的夹角为60°.
,则a,b的夹角为60°.
以上命题中,错误命题的序号是________.
 的夹角为θ,且
的夹角为θ,且 为正实数.
为正实数. 垂直,求tanθ;
垂直,求tanθ; 的模不小于
的模不小于 ,求θ的取值范围;
,求θ的取值范围; 有两个不同的正实数解,且x≠m,求m的取值范围.
有两个不同的正实数解,且x≠m,求m的取值范围.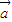 ,
,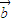 都有|
都有|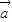 •
•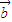 |=|
|=| |•|
|•| |;
|;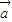 ,
,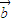 是两个不共线的向量,且
是两个不共线的向量,且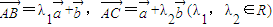 ,则A、B、C共线?λ1λ2=-1;
,则A、B、C共线?λ1λ2=-1;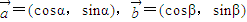 ,则
,则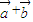 与
与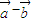 的夹角为90°;
的夹角为90°;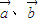 满足
满足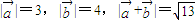 ,则
,则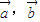 的夹角为60°.
的夹角为60°.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com