
题目列表(包括答案和解析)
| 1 | 2(1+β) |
| A、2 | B、6 | C、8 | D、10 |
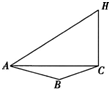 为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气象仪器,这种仪器可以弹射到空中进行气象观测.如图所示,A,B,C三地位于同一水平面上,这种仪器在C地进行弹射实验,观测点A,B两地相距100米,∠BAC=60°在A地听到弹射声音的时间比B地晚
为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气象仪器,这种仪器可以弹射到空中进行气象观测.如图所示,A,B,C三地位于同一水平面上,这种仪器在C地进行弹射实验,观测点A,B两地相距100米,∠BAC=60°在A地听到弹射声音的时间比B地晚| 2 | 17 |
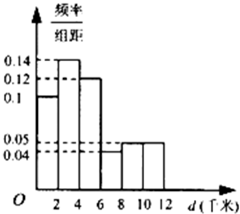 某公司为了改善职工的出行条件,随机抽取100名职工,调查了他们的居住地与公司间的距离d(单位:千米).由其数据绘制的频率分布直方图如图所示,则样本中职工居住地与公司间的距离不超过4千米的人数为
某公司为了改善职工的出行条件,随机抽取100名职工,调查了他们的居住地与公司间的距离d(单位:千米).由其数据绘制的频率分布直方图如图所示,则样本中职工居住地与公司间的距离不超过4千米的人数为湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com