
题目列表(包括答案和解析)
(2006年安徽卷)已知函数 在R上有定义,对任何实数
在R上有定义,对任何实数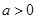 和任何实数
和任何实数 ,都有
,都有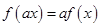
(Ⅰ)证明 ;
;
(Ⅱ)证明 其中
其中 和
和 均为常数;
均为常数;
(Ⅲ)当(Ⅱ)中的 时,设
时,设 ,讨论
,讨论 在
在 内的单调性并求极值.
内的单调性并求极值.
(08年安徽卷理)(本小题满分12分)
为防止风沙危害,某地决定建设防护绿化带,种植杨树、沙柳等植物。某人一次种植了![]() 株沙柳。各株沙柳的成活与否是相互独立的,成活率为
株沙柳。各株沙柳的成活与否是相互独立的,成活率为![]() ,设
,设![]() 为成活沙柳的株数,数学期望
为成活沙柳的株数,数学期望![]() 为3,标准差
为3,标准差![]() 为
为![]() 。
。
(Ⅰ)求![]() 的值,并写出
的值,并写出![]() 的分布列;
的分布列;
(Ⅱ)若有3株或3株以上的沙柳未成活,则需要补种,求需要补种沙柳的概率。
(07年安徽卷理)如图,![]() 和
和![]() 分别是双曲线
分别是双曲线![]() 的两个焦点,
的两个焦点,![]() 和
和![]() 是以
是以![]() 为圆心,以
为圆心,以![]() 为半径的圆与该双曲线左支的两个交点,且△
为半径的圆与该双曲线左支的两个交点,且△![]() 是等边三角形,则双曲线的离心率为
是等边三角形,则双曲线的离心率为

(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(07年安徽卷理)(本小题满分14分)
设a≥0,f (x)=x-1-ln2 x+2a ln x(x>0).
(Ⅰ)令F(x)=xf'(x),讨论F(x)在(0.+∞)内的单调性并求极值;
(Ⅱ)求证:当x>1时,恒有x>ln2x-2a ln x+1.
(08年安徽卷理)(本小题满分12分)
如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,![]() 底面
底面![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
(I)证明:直线![]() 平面
平面![]() .
.
(II)求异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
(III)求点![]() 到平面
到平面![]() 的距离.
的距离.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com