练习册

  • 练习册
  • 试题
    2．计算并完成以下表格 n -3 -2 -1 0 1 2 3 教学环节与问题设计 设计目的 第一环节:创设游戏情境.设疑激趣 学生分成小组.动手折纸 , 观察对折次数与所得纸的层数的关系.得出折一次为 2 层纸.折两次为 22层纸 , 折三次为 23 层纸 ...得对折次数x与所得纸的层数 y 的关系式为 y =2x 设疑激趣.在学生动手操作的过程中激发学生学习热情和探索新知的欲望. 第二环节:引出具体定义.探究条件 定义: 一般地 , 函数 = (且) 叫做指数函数 , 其中 是自变量 , 定义域为 R. 问题:为何对有这样的要求? (1) 如果=0 当 ＞0 时 恒等于 0; 当 〈 0 时 , 无意义 (2) 如果〈 0 时,比如: .对及等都无意义 (3) 如果 =1, 则原函数变成是一个常数 , 研究价值不大. 对a的范围的具体分析.有利于学生对指数函数一般形式的掌握.同时为后面研究函数的图象和性质埋下了伏笔. 第三环节:运用定义.判断具体函数 能否判断下列函数哪些是指数函数吗? (1) (2) (3) (4) 打破学生对定义的轻视并使学生头脑中不断完善对定义理解 【查看更多】

     

    题目列表(包括答案和解析)

    （2012•荆州模拟）OP是底部O不能到达的高塔，P是高塔的最高点，选择一条水平基线M，N，使得M，N，O三点在同一条直线上，在相距为d的M，N两点用测角仪测得P的仰角分别为α，β，已知测角仪高h=1.5m，试完成如下《实验报告》

    （要求：（1）计算两次测量值的平均值并填入表格；（2）利用α，β，d的平均值，求OP的值，写出详细的计算过程；
    （3）把计算结果填入表格．（相关数据：）

    题目 测量底部不能到达的高塔的高度 计算过程
    测量数据 测量项目 第一次 第二次 平均值
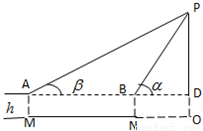
    α 75°32′ 74°28′
    β 30°17′ 29°43′
    d（m） 59.82 60.18
    测量目标
    结果

    查看答案和解析>>

    三角函数内容丰富，公式很多．如果你仔细观察、敢于设想、科学求证，那么你也能发现其中的一些奥秘．请你完成以下问题：
    （1）计算：（直接写答案）
    cos2°
    sin47°
    +
    cos88°
    sin133°
    =
    		2
    		2
    cos5°
    sin50°
    +
    cos85°
    sin130°
    =
    		2
    		2

    （2）根据（1）的计算结果，请你猜出一个一般性的结论：
    cos(θ-45°)
    sinθ
    +
    cos(135°-θ)
    sin(180°-θ)
    =
    		2
    cos(θ-45°)
    sinθ
    +
    cos(135°-θ)
    sin(180°-θ)
    =
    		2
    ．（用数学式子加以表达，并证明你的结论，写出推理过程．）

    查看答案和解析>>

    OP是底部O不能到达的高塔，P是高塔的最高点，选择一条水平基线M，N，使得M，N，O三点在同一条直线上，在相距为d的M，N两点用测角仪测得P的仰角分别为α，β，已知测角仪高h=1.5m，试完成如下《实验报告》

    （要求：（1）计算两次测量值的平均值并填入表格；（2）利用α，β，d的平均值，求OP的值，写出详细的计算过程；
    （3）把计算结果填入表格．（相关数据：）

    题目测量底部不能到达的高塔的高度计算过程
    测量数据测量项目第一次第二次平均值
    α75°32′74°28′
    β30°17′29°43′
    d（m）59.8260.18
    测量目标
    结果

    查看答案和解析>>

    探究函数f(x)=2x+
    8
    x
    ，x∈(0，+∞)    的最小值，并确定取得最小值时x的值．列表如下：
    x … 0.5 1 1.5 1.7 1.9 2 2.1 2.2 2.3 3 4 5 7 …
    y … 16 10 8.34 8.1 8.01 8 8.01 8.04 8.08 8.6 10 11.6 15.14 …
    请观察表中y值随x值变化的特点，完成以下的问题．
    （1）函数f(x)=2x+
    8
    x
    (x＞0)    在区间（0，2）上递减；函数f(x)=2x+
    8
    x
    (x＞0)    在区间
    （2，+∞）
    （2，+∞）
    上递增．当x=
    2
    2
    时，y最小=
    4
    4
    ．
    （2）证明：函数f(x)=2x+
    8
    x
    (x＞0)    在区间（0，2）递减．
    （3）思考：函数f(x)=2x+
    8
    x
    (x＜0)    时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）

    查看答案和解析>>

    探究函数f（x）=x+
    4
    x
    ，x∈（0，+∞）的最小值，并确定取得最小值时x的值．列表如下：
    x … 0.5 1 1.5 1.7 1.9 2 2.1 2.2 2.3 3 4 5 7 …
    y … 8.5 5 4.17 4.05 4.005 4 4.005 4.02 4.04 4.3 5 5.8 7.57 …
    请观察表中值y随x值变化的特点，完成以下的问题．
    函数f（x）=x+
    4
    x
    （x＞0）在区间（0，2）上递减；
    函数f（x）=x+
    4
    x
    （x＞0）在区间
    （2，0）
    （2，0）
    上递增．
    当x=
    2
    2
    时，y最小=
    4
    4
    ．
    证明：函数f（x）=x+
    4
    x
    （x＞0）在区间（0，2）递减．
    思考：（直接回答结果，不需证明）
    （1）函数f（x）=x+
    4
    x
    （x＜0）有没有最值？如果有，请说明是最大值还是最小值，以及取相应最值时x的值．
    （2）函数f（x）=ax+
    b
    x
    ，（a＜0，b＜0）在区间
    [-
    b
    a
    ，0）
    [-
    b
    a
    ，0）
     和
    （0，
    b
    a
    ]
    （0，
    b
    a
    ]
    上单调递增．

    查看答案和解析>>


    同步练习册答案