题目列表(包括答案和解析)
Sh（S为底面积，h为锥体高），锥体的高是指（ ）；
（S'+
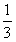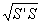+S）h（S'，S分别为上、下底面面积，h为台体高），台体的高是指（ ）。
圆柱、圆锥的底面半径与球的半径都为r，圆柱、圆锥的高都是2r．求它们的体积之比．
斜三棱柱
中，侧面
底面ABC，侧面是菱形，
，
，
，E、F分别是
，AB的中点．
（1）求证：EF∥平面
；
（2）求证：CE⊥面ABC．
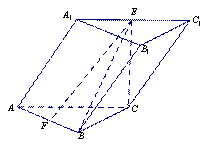（3）求四棱锥
的体积．.
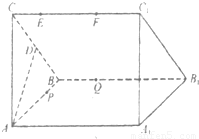
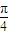
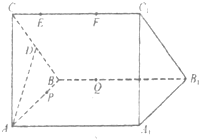设直三梭柱ABC-A1B1C1的底面为等腰直角三角形，AB=AC=2，动点E、F在侧棱CC1上，动点P、Q分别碰AB1，BB1上，若EF═1，CE=x，BQ=y，BP=z，其中x，y，z＞0，则下列结论中错误的是．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com