
题目列表(包括答案和解析)
(09年大丰调研)(10分)
设![]() 是把坐标平面上的点的横坐标伸长到
是把坐标平面上的点的横坐标伸长到![]() 倍,纵坐标伸长到
倍,纵坐标伸长到![]() 倍的伸压变换.
倍的伸压变换.
(Ⅰ)求矩阵![]() 的特征值及相应的特征向量;
的特征值及相应的特征向量;
(Ⅱ)求逆矩阵![]() 以及椭圆
以及椭圆![]() 在
在![]() 的作用下的新曲线的方程.
的作用下的新曲线的方程.
| x2 |
| 4 |
| y2 |
| 9 |
| x2 |
| 4 |
| y2 |
| 9 |
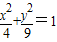 在M-1的作用下的新曲线的方程.
在M-1的作用下的新曲线的方程.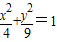 在M-1的作用下的新曲线的方程.
在M-1的作用下的新曲线的方程.一、填空题
1. ;2.-1;3.48;4.
;2.-1;3.48;4. ;5.1;6.a
;5.1;6.a
 ;7.
;7. ;
;
8. ;9.
;9. ;10.4;11.160;12.
;10.4;11.160;12. ;13.
;13. ;14.
;14. .
.
二、解答题
15.证明:(Ⅰ)
因为平面PBC与平面PAD的交线为

所以
(Ⅱ)在 中,由题设
中,由题设 可得
可得
 于是
于是
在矩形 中,
中, .又
.又 ,
,
所以 平面
平面 又
又
即 平面PBC与平面PAD所成二面角的一个平面角
平面PBC与平面PAD所成二面角的一个平面角
在 中
中 

所以平面PBC与平面PAD所成二面角的大小为 .
.
16.解:(Ⅰ)
 ……2分
……2分
由题意得 ,
, ,得
,得 ,
,
当 时,最小正整数
时,最小正整数 的值为2,故
的值为2,故 . ……6分
. ……6分
(Ⅱ)因 且
且 
则 当且仅当
当且仅当 ,
, 时,等号成立
时,等号成立
则 ,又因
,又因 ,则
,则 ,即
,即  ……10分
……10分
由①知:
因 ,则
,则  ,
, 
 ,故函数
,故函数 的值域为
的值域为 .
……14分
.
……14分
当x=1时,g(x)=g(1)也适合上式
等号当且仅当x=12-x即x=6时成立,即当x=6时, (万件)
(万件)
18.解:(Ⅰ) 由(x-12)2+y2=144-a(a<144),可知圆心M的坐标为(12,0),
依题意,∠ABM=∠BAM=,kAB= , 设MA、MB的斜率k.
则 且
且 , 解得
, 解得 =2,
=2, =- .
=- .
∴所求BD方程为x+2y-12=0,AC方程为2x-y-24=0.
(Ⅱ) 设MB、MA的倾斜角分别为θ1,θ2,则tanθ1=2,tanθ2=-,
设圆半径为r,则A(12+ ),B(12-
),B(12- ,
, ),
),
再设抛物线方程为y2=2px (p>0),由于A,B两点在抛物线上,
∴ ∴ r=4,p=2.
得抛物线方程为y2=4x。
19.解:(Ⅰ)设数列 的公差为
的公差为 ,由
,由
 ,
,
 ,解得
,解得 ,
, =3
=3
∴
∵ ∴Sn=
∴Sn= =
=
(Ⅱ) 
∴
∴
(Ⅲ)由(2)知,
∴ ,
,
∵ 成等比数列
成等比数列
∴  即
即
当 时,7
时,7 ,
, =1,不合题意;
=1,不合题意;
当 时,
时,
 ,
, =16,符合题意;
=16,符合题意;
当 时,
时,
 ,
, 无正整数解;
无正整数解;
当 时,
时,
 ,
, 无正整数解;
无正整数解;
当 时,
时,
 ,
, 无正整数解;
无正整数解;
当 时,
时,
 ,
, 无正整数解;
无正整数解;
当 时,
时, ,则
,则 ,而
,而 ,所以,此时不存在正整数m,n,且1<m<n,使得
,所以,此时不存在正整数m,n,且1<m<n,使得 成等比数列。
成等比数列。
综上,存在正整数m=2,n=16,且1<m<n,使得 成等比数列。
成等比数列。
20.解:(Ⅰ)假设 ①,其中
①,其中 偶函数,
偶函数, 为奇函数,则有
为奇函数,则有 ,即
,即 ②,
②,
由①②解得 ,
, .
.
∵ 定义在R上,∴
定义在R上,∴ ,
, 都定义在R上.
都定义在R上.
∵ ,
, .
.
∴ 是偶函数,
是偶函数, 是奇函数,
是奇函数,
∵ ,
,
∴ ,
,
 .
.
由 ,则
,则 ,
,
平方得 ,∴
,∴ ,
,
∴ .
…………6分
.
…………6分
(Ⅱ)∵ 关于
关于 单调递增,∴
单调递增,∴ .
.
∴ 对于
对于 恒成立,
恒成立,
∴ 对于
对于 恒成立,
恒成立,
令 ,则
,则 ,
,
∵ ,∴
,∴ ,故
,故 在
在 上单调递减,
上单调递减,
∴ ,∴
,∴ 为m的取值范围. …………10分
为m的取值范围. …………10分
(Ⅲ)由(1)得 ,
,
若 无实根,即
无实根,即 ①无实根,
①无实根,
方程①的判别式 .
.
1°当方程①的判别式 ,即
,即 时,
时,
方程①无实根. ……………12分
2°当方程①的判别式 ,即
,即 时,
时,
方程①有两个实根 ,
,
即 ②,
②,
只要方程②无实根,故其判别式 ,
,
即得 ③,且
③,且 ④,
④,
∵ ,③恒成立,由④解得
,③恒成立,由④解得 ,
,
∴③④同时成立得 .
.
综上,m的取值范围为 . ……………16分
. ……………16分
 三、附加题
三、附加题
∵ÐDEF是公共角,
∴ΔDEF∽ΔCED. ∴ÐEDF=ÐC.
∵CD∥AP, ∴ÐC=Ð P.
∴ÐP=ÐEDF.
(2)∵ÐP=ÐEDF, ÐDEF=ÐPEA,
∴ΔDEF∽ΔPEA. ∴DE : PE=EF : EA.即EF?EP=DE?EA.
∵弦AD、BC相交于点E,∴DE?EA=CE?EB.∴CE?EB=EF?EP.
21B.解(Ⅰ)由条件得矩阵 ,
,
它的特征值为 和
和 ,对应的特征向量为
,对应的特征向量为 及
及 ;
;
(Ⅱ) ,
,
椭圆 在
在 的作用下的新曲线的方程为
的作用下的新曲线的方程为 .
.


(Ⅱ)x+y=4+2sin( ) 最大值6,最小值2 .
) 最大值6,最小值2 .
21D.证明:



当且仅当 时,等号成立.
时,等号成立.
22.解:设既会唱歌又会跳舞的有x人,则文娱队中共有(7-x)人,那么只会一项的人数是(7-2 x)人.
(I)∵ ,
,
∴ .即
.即 .
.
∴ .
.
∴x=2. 故文娱队共有5人.
(II)  ,
, ,
,
 的概率分布列为
的概率分布列为

0
1
2
P



∴ =1.
=1.
23.解:(Ⅰ) ;
;
(Ⅱ) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com