
题目列表(包括答案和解析)
(2012年高考(浙江文))已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积是 ( )
A.1cm3 B.2cm3
C.3cm3 D.6cm3

(09浙江文19.)如图, 平面
平面 ,
, ,
, ,
,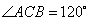 ,
, 分别为
分别为 的中点.
的中点.
 (I)证明:
(I)证明: 平面
平面 ;
;
(II)求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
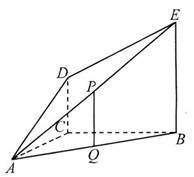
(2004
浙江,10)如下图,在正三棱柱ABC- 中,已知AB=1,D在棱
中,已知AB=1,D在棱 上,且BD=1,若AD与平面
上,且BD=1,若AD与平面 所成的角为α,则α等于
所成的角为α,则α等于

[
]|
A . |
B . |
|
C .arcsin |
D .arcsin |
(2004
浙江,22)如图所示,△OBC的三个顶点坐标分别为(0,0)、(1,0)、(0,2),设 为线段BC的中点,
为线段BC的中点, 为线段CO的中点,
为线段CO的中点, 为线段
为线段 的中点,对于每一个正整数n,
的中点,对于每一个正整数n, 为线段
为线段 的中点,令
的中点,令 的坐标为
的坐标为 ,
, .
.
(1)
求 ;
;
(2)
证明: ,
, ;
;
(3)
若记 ,
, ,证明
,证明 是等比数列.
是等比数列.

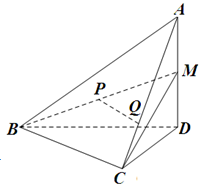 (2013•浙江)如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2
(2013•浙江)如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com