0＜α＜1,0＜β＜1，数列{x_n},{y_n}由以下条件确定：(x₁,y₁)=(2,1),(x_n+1,y_n+1)=(αx_n+1-α,βy_n+2-2β), (n=1,2,3,…)完成以下问题.

(1)求数列{x_n}与{y_n}的通项；

(2)求x_n，y_n；

(3)数列{x_n},{y_n}是有限数列时，当α=β时，求点(x_n,y_n)的存在范围；

(4)数列{x_n},{y_n}是有限数列时，当β≥α²时，将点(x_n,y_n)的存在范围用图形表示出来.

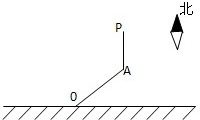在东西方向直线延伸的湖岸上有一港口O，一艘机艇以40km/h的速度从O港出发，先沿东偏北的某个方向直线前进到达A处，然后改向正北方向航行，总共航行30分钟因机器出现故障而停在湖里的P处，由于营救人员不知该机艇的最初航向及何时改变的航向，故无法确定机艇停泊的准确位置，试划定一个最佳的弓形营救区域（用图形表示），并说明你的理由．

A、（-1，1]

B、[-1，1）

C、（-1，1）

D、[-1，1]

设有圆心为(a_k,0),半径为r_k(k=1,2,…)的一系列半圆C₁,C₂,C₃,…,每相邻半圆互相外切,并且都和直线y=-x+1相切.

(1)用r_k表示a_k;

(2)用r_k-1表示r_k;

(3)若a₁＜0,半圆C₁和y轴相切,求r₁;

(4)在(3)中的半圆C₁是这一系列半圆的左起第一个半圆,面积为S₁,第k个半圆的面积为S_k,求S₁+S₂+S₃+…+S_k+….

如右图,一个结晶体的形状为平行六面体，以点为端点的三条棱

的长都等于，且彼此之间的夹角都是.

(1)用向量表示向量.

(2)求晶体的对角线长.