
题目列表(包括答案和解析)
如图所示是从一批产品中抽样得到的数据的频率分布直方图,由图形可以看出数据所落在范围的概率最大的是
A.(8.1,8.3) B.(8.2,8.4)
C.(8.4,8.5) D.(8.5,8.7)

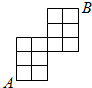 如图所示是某个区域的街道示意图(每个小矩形的边表示街道),则从A到B的最短线路有( )条.
如图所示是某个区域的街道示意图(每个小矩形的边表示街道),则从A到B的最短线路有( )条.
| 2 | 3 |
 19、从某学校高三年级共800名男生中随机抽取50人测量身高.据测量被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…;第八组[190,195].如图所示是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
19、从某学校高三年级共800名男生中随机抽取50人测量身高.据测量被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…;第八组[190,195].如图所示是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.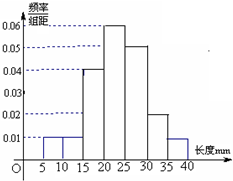 某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示.从抽样的100根棉花纤维中任意抽取一根,则其棉花纤维的长度小于20mm的概率为
某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示.从抽样的100根棉花纤维中任意抽取一根,则其棉花纤维的长度小于20mm的概率为| 3 |
| 10 |
| 3 |
| 10 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com