
题目列表(包括答案和解析)
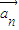 ,n∈N*,满足:
,n∈N*,满足: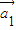 =(10,-5),
=(10,-5),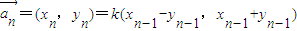 ,(n32 ).,其中k是非零常数.
,(n32 ).,其中k是非零常数.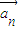 |}是的通项公式;
|}是的通项公式;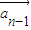 与
与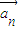 的夹角;(n≥2);
的夹角;(n≥2); 时,把
时,把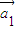 ,
,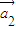 ,…,
,…,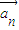 ,…中所有与
,…中所有与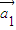 共线的向量按原来的顺序排成一列,记为
共线的向量按原来的顺序排成一列,记为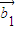 ,
,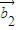 ,…,
,…,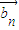 ,…,令
,…,令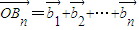 ,O为坐标原点,求点列{Bn}的极限点B的坐标.(注:若点坐标为(tn,sn),且
,O为坐标原点,求点列{Bn}的极限点B的坐标.(注:若点坐标为(tn,sn),且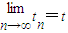 ,
,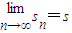 ,则称点B(t,s)为点列的极限点.)
,则称点B(t,s)为点列的极限点.)| S1 |
| 1 |
| S2 |
| 2 |
| S3 |
| 3 |
| Sn |
| n |
 在同一直线l1上;
在同一直线l1上;| S1 |
| 1 |
| S2 |
| 2 |
| S3 |
| 3 |
| Sn |
| n |
| an |
| a1 |
| an |
| an |
| an-1 |
| an |
| 1 |
| 2 |
| a1 |
| a2 |
| an |
| a1 |
| b1 |
| b2 |
| bn |
| OBn |
| b1 |
| b2 |
| bn |
| lim |
| n→∞ |
| lim |
| n→∞ |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com