
题目列表(包括答案和解析)
利用导数判断函数单调性的基本步骤:
(1)_________;
(2)_________;
(3)_________;
(4)_________.
已知函数 其中a>0.
其中a>0.
(I)求函数f(x)的单调区间;
(II)若函数f(x)在区间(-2,0)内恰有两个零点,求a的取值范围;
(III)当a=1时,设函数f(x)在区间[t,t+3]上的最大值为M(t),最小值为m(t),记g(t)=M(t)-m(t),求函数g(t)在区间[-3,-1]上的最小值。
【考点定位】本小题主要考查导数的运算,利用导数研究函数的单调性、函数的零点,函数的最值等基础知识.考查函数思想、分类讨论思想.考查综合分析和解决问题的能力.
已知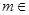 R,函数
R,函数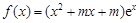 .
.
⑴若函数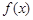 没有零点,求实数
没有零点,求实数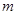 的取值范围;
的取值范围;
⑵若函数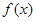 存在极大值,并记为
存在极大值,并记为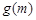 ,求
,求 的表达式;
的表达式;
⑶当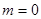 时,求证:
时,求证: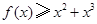 .
.
【解析】(1)求导研究函数f(x)的最值,说明函数f(x)的最大值<0,或f(x)的最小值>0.
(2)根据第(1)问的求解过程,直接得到g(m).
(3)构造函数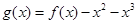 ,证明
,证明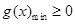 即可,然后利用导数求g(x)的最小值.
即可,然后利用导数求g(x)的最小值.
商场销售某种商品的经验表明,该商品每日的销售量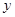 (单位:千克)与销售价格
(单位:千克)与销售价格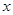 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式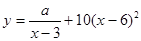 ,其中
,其中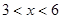 ,
,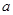 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
(1) 求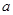 的值;
的值;
(2) 若商品的成品为3元/千克, 试确定销售价格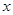 的值,使商场每日销售该商品所获得的利润最大
的值,使商场每日销售该商品所获得的利润最大
【解析】(1)利用销售价格为5元/千克时,每日可售出该商品11千克.把x=5,y=11代入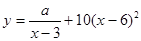 ,解关于a的方程即可求a..
,解关于a的方程即可求a..
(2)在(1)的基础上,列出利润关于x的函数关系式,
利润=销售量 (销售单价-成品单价),然后利用导数求其最值即可.
(销售单价-成品单价),然后利用导数求其最值即可.
已知函数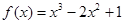 .
.
(1)求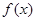 在区间
在区间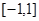 上的最大值;
上的最大值;
(2)若函数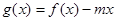 在区间
在区间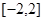 上存在递减区间,求实数m的取值范围.
上存在递减区间,求实数m的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用,求解函数的最值。第一问中,利用导数求解函数的最值,首先求解导数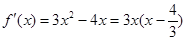 ,然后利用极值和端点值比较大小,得到结论。第二问中,我们利用函数在
,然后利用极值和端点值比较大小,得到结论。第二问中,我们利用函数在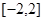 上存在递减区间,即
上存在递减区间,即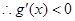 在
在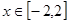 上有解,即
上有解,即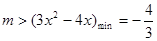 ,即可,可得到。
,即可,可得到。
解:(1)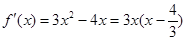 ,
,
令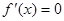 ,解得
,解得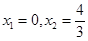 ……………3分
……………3分
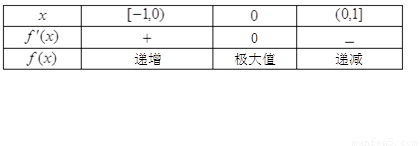
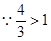 ,
,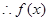 在
在 上为增函数,在
上为增函数,在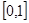 上为减函数,
上为减函数,
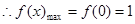 .
…………6分
.
…………6分
(2)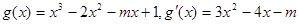
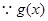 在
在 上存在递减区间,
上存在递减区间,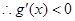 在
在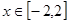 上有解,……9分
上有解,……9分
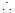
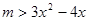 在
在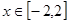 上有解,
上有解,
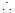
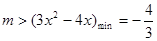 ,
,
所以,实数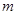 的取值范围为
的取值范围为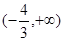
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com