
题目列表(包括答案和解析)
为了解某班学生喜爱打羽毛球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
|
|
喜爱打羽毛球 |
不喜爱打羽毛球 |
合计 |
|
男生 |
|
5 |
|
|
女生 |
10 |
|
|
|
|
|
|
50 |
已知在全部50人中随机抽取1人抽到不喜爱打羽毛球的学生的概率
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打羽毛球与性别有关?说明你的理由;
(3)已知喜爱打羽毛球的10位女生中, 还喜欢打篮球,
还喜欢打篮球, 还喜欢打乒乓球,
还喜欢打乒乓球, 还喜欢踢足球,现在从喜欢打篮球、喜欢打乒乓球、喜欢踢足球的6位女生中各选出1名进行其他方面的调查,求女生
还喜欢踢足球,现在从喜欢打篮球、喜欢打乒乓球、喜欢踢足球的6位女生中各选出1名进行其他方面的调查,求女生 和
和 不全被选中的概率.下面的临界值表供参考:
不全被选中的概率.下面的临界值表供参考:
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: 其中
其中 .)
.)
【解析】第一问利用数据写出列联表
第二问利用公式 计算的得到结论。
计算的得到结论。
第三问中,从6位女生中选出喜欢打篮球、喜欢打乒乓球、喜欢踢足球的各1名,其一切可能的结果组成的基本事件如下:
 ,
,
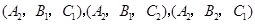 ,
,
基本事件的总数为8
用 表示“
表示“ 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件 表示“
表示“ 全被选中”这一事件,由于
全被选中”这一事件,由于 由
由 2个基本事件由对立事件的概率公式得
2个基本事件由对立事件的概率公式得
解:(1) 列联表补充如下:
|
|
喜爱打羽毛球 |
不喜爱打羽毛球 |
合计 |
|
男生 |
20 |
5 |
25 |
|
女生 |
10 |
15 |
25 |
|
合计 |
30 |
20 |
50 |
(2)∵
∴有99.5%的把握认为喜爱打篮球与性别有关
(3)从6位女生中选出喜欢打篮球、喜欢打乒乓球、喜欢踢足球的各1名,其一切可能的结果组成的基本事件如下:
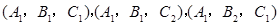 ,
,
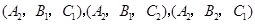 ,
,
基本事件的总数为8,
用 表示“
表示“ 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件 表示“
表示“ 全被选中”这一事件,由于
全被选中”这一事件,由于 由
由 2个基本事件由对立事件的概率公式得
2个基本事件由对立事件的概率公式得 .
.
独立重复试验中,某事件恰好发生k次的概率公式为![]() ,它与
,它与![]() 的展开式中第 项系数及其类似,此时a= ,b= ,x= .
的展开式中第 项系数及其类似,此时a= ,b= ,x= .
某校从参加高三年级理科综合物理考试的学生中随机抽出 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段 ,
, …
… 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求分数在 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的
平均分;
(Ⅲ)若从 名学生中随机抽取
名学生中随机抽取 人,抽到的学生成绩在
人,抽到的学生成绩在 记
记 分,在
分,在 记
记 分,
分,
在 记
记 分,用
分,用 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求 的分布列和数学期望.
的分布列和数学期望.

【解析】(1)中利用直方图中面积和为1,可以求解得到分数在 内的频率为
内的频率为
(2)中结合平均值可以得到平均分为:
(3)中用 表示抽取结束后的总记分x, 学生成绩在
表示抽取结束后的总记分x, 学生成绩在 的有
的有 人,在
人,在 的有
的有 人,在
人,在 的有
的有 人,结合古典概型的概率公式求解得到。
人,结合古典概型的概率公式求解得到。
(Ⅰ)设分数在 内的频率为
内的频率为 ,根据频率分布直方图,则有
,根据频率分布直方图,则有 ,可得
,可得 ,所以频率分布直方图如右图.……4分
,所以频率分布直方图如右图.……4分


(求解频率3分,画图1分)
(Ⅱ)平均分为: ……7分
……7分
(Ⅲ)学生成绩在 的有
的有 人,在
人,在 的有
的有 人,
人,
在 的有
的有 人.并且
人.并且 的可能取值是
的可能取值是 . ………8分
. ………8分
则 ;
; ;
;
 ;
;
 ;
; .(每个1分)
.(每个1分)
所以 的分布列为
的分布列为
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
…………………13分

学校要用三辆车从北湖校区把教师接到文庙校区,已知从北湖校区到文庙校区有两条公路,汽车走公路①堵车的概率为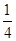 ,不堵车的概率为
,不堵车的概率为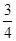 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为 ,不堵车的概率为
,不堵车的概率为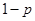 ,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为
,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为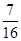 ,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数
,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数 的分布列和数学期望。
的分布列和数学期望。
【解析】第一问中,由已知条件结合n此独立重复试验的概率公式可知,得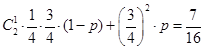
第二问中 可能的取值为0,1,2,3
可能的取值为0,1,2,3 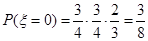 ,
, 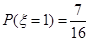
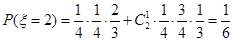 ,
,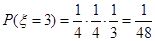
从而得到分布列和期望值
解:(I)由已知条件得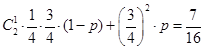 ,即
,即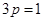 ,则
,则 的值为
的值为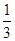 。
。
(Ⅱ) 可能的取值为0,1,2,3
可能的取值为0,1,2,3 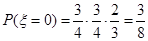 ,
, 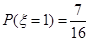
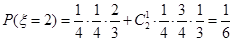 ,
,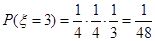
 的分布列为:(1分)
的分布列为:(1分)
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
所以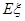
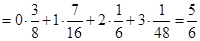
古典概型的概率公式
对于任何事件A,P(A)=________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com