
题目列表(包括答案和解析)
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 4 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
某项选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为![]() 、
、![]() 、
、![]() ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数数期望.(注:本小题结果可用分数表示)
(本题满分12分)某项竞赛分别为初赛、复赛、决赛三个阶段进行,每个阶段选手要
回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是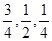 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(1)求该选手在复赛阶段被淘汰的概率;
(2)设该选手在竞赛中回答问题的个数为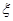 ,求
,求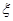 的分布列、数学期望和方差.
的分布列、数学期望和方差.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com