练习册

  • 练习册
  • 试题
    重点:交集与并集.全集与补集的概念. 难点:理解交集与并集的概念.符号之间的区别与联系． 【查看更多】

     

    题目列表(包括答案和解析)

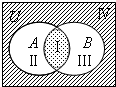    1、设全集为U，用集合A、B的交集、并集、补集分别表示如图韦恩图中Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分为：Ⅰ部分：A∩B，Ⅱ部分：A∩CUB，Ⅲ部分：B∩CU（A∩B），Ⅳ部分：CU（A∩B），其中表示错误的是（　　）

    查看答案和解析>>

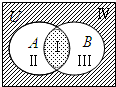    设全集为U，用集合A、B的交集、并集、补集分别表示右边韦恩图中Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分为：Ⅰ部分：A∩B，Ⅱ部分：A∩CUB，Ⅲ部分：B∩CU（A∩B），Ⅳ部分：（CUA）∪（CUB），其中表示错误的是（　　）

    查看答案和解析>>

    如下图，有四个区域Ⅰ、Ⅱ、Ⅲ、Ⅳ.下面给出了四个用集合A、B的交集、并集、补集表示的集合，请你将对应的集合与区域连结起来.

    B∩（A）                            Ⅰ

    A∩B                                      Ⅱ

    A∩（B）                            Ⅲ

    *（A∪B）                            Ⅳ

    查看答案和解析>>

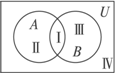
    如图，有四个区域Ⅰ、Ⅱ、Ⅲ、Ⅳ分别代表与A、B有关的交集、并集、补集，请你将对应的集合与区域连结起来．

    查看答案和解析>>

    已知集合A={x|x2-4x+3＜0}，B={x||x-3|≤1}，
    （1）请根据集合的交集、并集、补集等运算性质的特征，设计一种集合运算：△，可以使A△B={x|1＜x＜2}并用集合的符号语言来表示A△B；
    （2）按（1）中所确定的运算，求出B△A．

    查看答案和解析>>


    同步练习册答案