
题目列表(包括答案和解析)
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
| 1 |
| 2 |
| OP |
| OA |
| ||
|
|
| ||
|
|
| OP |
| OP |
| ||||
| 2 |
| ||
|
|
| ||
|
|
| OP |
| ||||
| 2 |
| ||
|
|
| ||
|
|
| 1 |
| x |
| 1 |
| xn |
 ,并且当n>1且n∈N*时,满足
,并且当n>1且n∈N*时,满足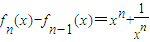 .
.建立数学模型一般都要经历下列过程:从实际情境中提出问题,建立数学模型,通过计算或推导得到结果,结合实际情况进行检验.如果合乎实际,就得到可以应用的结果,否则重新审视问题的提出、建模、计算和推导得到结果的过程,直到得到合乎实际的结果为止.请设计一个流程图表示这一过程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com