
题目列表(包括答案和解析)
 (2009•闵行区二模)(理)在长方体ABCD-A1B1C1D1中,AB=2,AD=1,AA1=1,点E在棱AB上移动.
(2009•闵行区二模)(理)在长方体ABCD-A1B1C1D1中,AB=2,AD=1,AA1=1,点E在棱AB上移动. (2012•江苏二模)如图,已知椭圆C:
(2012•江苏二模)如图,已知椭圆C:| x2 |
| 4 |
| OP |
| OA |
| OB |
| 1 |
| 2 |
| 3 |
| 2 |
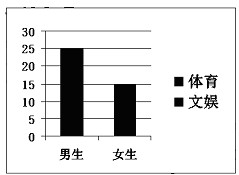 对某班学生是更喜欢体育还是更喜欢文娱进行调查,根据调查得到的数据,所绘制的二维条形图如图.
对某班学生是更喜欢体育还是更喜欢文娱进行调查,根据调查得到的数据,所绘制的二维条形图如图.| 1 | e |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com