
题目列表(包括答案和解析)
 (06年广东卷)(17 分)在光滑绝缘的水平桌面上,有两个质量均为m,电量为+q的完全相同的带电粒子P1和P2,在小孔A处以初速度为零先后释放。在平行板间距为d的匀强电场中加速后,P1从C处对着圆心进入半径为R的固定圆筒中(筒壁上的小孔C只能容一个粒子通过),圆筒内有垂直水平面向上的磁感应强度为B的匀强磁场。P1每次与筒壁发生碰撞均无电荷迁移,P1进入磁场第一次与筒壁碰撞点为D,∠COD=θ,如图12所示。延后释放的P2,将第一次欲逃逸出圆筒的P1正碰圆筒内,此次碰撞刚结束,立即改变平行板间的电压,并利用P2与P1之后的碰撞,将P1限制在圆筒内运动。碰撞过程均无机械能损失。设d=
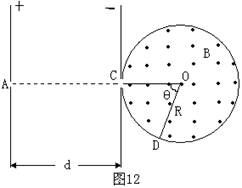
(06年广东卷)(17 分)在光滑绝缘的水平桌面上,有两个质量均为m,电量为+q的完全相同的带电粒子P1和P2,在小孔A处以初速度为零先后释放。在平行板间距为d的匀强电场中加速后,P1从C处对着圆心进入半径为R的固定圆筒中(筒壁上的小孔C只能容一个粒子通过),圆筒内有垂直水平面向上的磁感应强度为B的匀强磁场。P1每次与筒壁发生碰撞均无电荷迁移,P1进入磁场第一次与筒壁碰撞点为D,∠COD=θ,如图12所示。延后释放的P2,将第一次欲逃逸出圆筒的P1正碰圆筒内,此次碰撞刚结束,立即改变平行板间的电压,并利用P2与P1之后的碰撞,将P1限制在圆筒内运动。碰撞过程均无机械能损失。设d=![]() ,求:在P2和P1相邻两次碰撞时间间隔内,粒子P1与筒壁的可能碰撞次数。
,求:在P2和P1相邻两次碰撞时间间隔内,粒子P1与筒壁的可能碰撞次数。
附:部分三角函数值
|
|
|
|
|
|
|
|
|
|
tan | 3.08 | 1.37 | 1.00 | 0.73 | 0.58 | 0.48 | 0.41 | 0.36 | 0.32 |
(06年广东卷)(16分)宇宙中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其它星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为R的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个项点上,并沿外接于等边三角形的圆形轨道运行。设每个星体的质量均为![]() 。
。
(1)试求第一种形式下,星体运动的线速度和周期。
(2)假设两种形式星体的运动周期相同,第二种形式下星体之间的距离应为多少?
(06年广东卷)(16分)宇宙中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其它星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为R的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个项点上,并沿外接于等边三角形的圆形轨道运行。设每个星体的质量均为![]() 。
。
(1)试求第一种形式下,星体运动的线速度和周期。
(2)假设两种形式星体的运动周期相同,第二种形式下星体之间的距离应为多少?
| Lu |
| I |
| Lu |
| I |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com