
题目列表(包括答案和解析)
(1)当m∈(1,2)时,求|![]() |的最大值,并求出此时的椭圆C方程;
|的最大值,并求出此时的椭圆C方程;
(2)在(1)的条件下,过点P的直线l与椭圆C相交于M、N两点,与椭圆C对应于焦点P的准线相交于D点,且![]() =λ1
=λ1![]() ,
,![]() =λ2
=λ2![]() 请找出λ1、λ2之间的关系,并证明你的结论.
请找出λ1、λ2之间的关系,并证明你的结论.
| m |
| 3 |
| n |
| m |
| n |
已知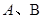 是圆
是圆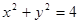 上满足条件
上满足条件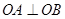 的两个点,其中O是坐标原点,分别过A、B作
的两个点,其中O是坐标原点,分别过A、B作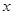 轴的垂线段,交椭圆
轴的垂线段,交椭圆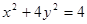 于
于 点,动点P满足
点,动点P满足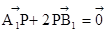 .(1)求动点P的轨迹方程;(2)设
.(1)求动点P的轨迹方程;(2)设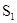 和
和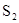 分别表示
分别表示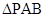 和
和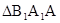 的面积,当点P在
的面积,当点P在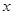 轴的上方,点A在
轴的上方,点A在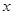 轴的下方时,求
轴的下方时,求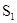 +
+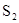 的最大值。
的最大值。
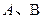 是圆
是圆 上满足条件
上满足条件 的两个点,其中O是坐标原点,分别过A、B作
的两个点,其中O是坐标原点,分别过A、B作 轴的垂线段,交椭圆
轴的垂线段,交椭圆 于
于 点,动点P满足
点,动点P满足 .(1)求动点P的轨迹方程;(2)设
.(1)求动点P的轨迹方程;(2)设 和
和 分别表示
分别表示 和
和 的面积,当点P在
的面积,当点P在 轴的上方,点A在
轴的上方,点A在 轴的下方时,求
轴的下方时,求 +
+ 的最大值。
的最大值。已知A、B是圆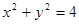 上满足条件
上满足条件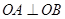 的两个点,其中O是坐标原点,
的两个点,其中O是坐标原点, 分别过A、B作
分别过A、B作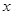 轴的垂线段,交椭圆
轴的垂线段,交椭圆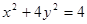 于
于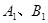 点,动点P满足
点,动点P满足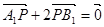 .(1)求动点P的轨迹方程;(2)设S1和S2
.(1)求动点P的轨迹方程;(2)设S1和S2 分别表示
分别表示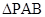 和
和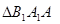 的面积,当点P在x轴的上方,点A在x轴的下方时,求
的面积,当点P在x轴的上方,点A在x轴的下方时,求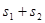 的最大值。
的最大值。
一、
二、
9.16 10.2009 11. 12.
12.
13. 14.3
14.3  15.②③
15.②③
三、
16.解:(1)由余弦定理得: 

 是以角C为直角的直角三角形.……………………6分
是以角C为直角的直角三角形.……………………6分
(2) 中
中
 ………………①
………………①
 ………………②
………………②
②÷①得 ,
,
则 ……………………12分
……………………12分
17.解:(1)因为 ……………………………………(2分)
……………………………………(2分)
 ……………………………………………………(4分)
……………………………………………………(4分)

所以线路信息通畅的概率为 。………………………(6分)
。………………………(6分)
(2) 的所有可能取值为4,5,6,7,8。
的所有可能取值为4,5,6,7,8。

 ……………………………………………………………(9分)
……………………………………………………………(9分)
∴ 的分布列为
的分布列为

4
5
6
7
8
P





…………………………………………………………………………………………(10分)
∴E =4×
=4× +5×
+5× +6×
+6× +7×
+7× +8×
+8× =6。……………………(12分)
=6。……………………(12分)
18.解:解法一:(1)证明:连结OC,
∵ ABD为等边三角形,O为BD的中点,∴AO
ABD为等边三角形,O为BD的中点,∴AO
垂直BD。………………………………………………………………(1分)
∴ AO=CO= 。………………………………………………………………………(2分)
。………………………………………………………………………(2分)
在 AOC中,AC=
AOC中,AC= ,∴AO2+CO2=AC2,
,∴AO2+CO2=AC2,
∴∠AOC=900,即AO⊥OC。
∴BD OC=O,∴AO⊥平面BCD。…………………………………………………(3分)
OC=O,∴AO⊥平面BCD。…………………………………………………(3分)
(2)过O作OE垂直BC于E,连结AE,
∵AO⊥平面BCD,∴AE在平面BCD上的射影为OE。
∴AE⊥BC。
∠AEO为二面角A―BC―D的平面角。………………………………………(7分)
在Rt AEO中,AO=
AEO中,AO= ,OE=
,OE= ,
,
 ∠
∠ ,
,
∴∠AEO=arctan2。
二面角A―BC―D的大小为arctan2。
(3)设点O到面ACD的距离为 ∵VO-ACD=VA-OCD,
∵VO-ACD=VA-OCD,
∴ 。
。
在 ACD中,AD=CD=2,AC=
ACD中,AD=CD=2,AC= ,
,
 。
。
|