题目列表(包括答案和解析)
考试结束，请将本试题卷和答题卡一并上交。
一、选择题(本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的)
1．设全集
，集合
，
，则图中的阴影部分表示的集合为
A．
B．
C．
D．
2．已知非零向量
、
满足
，那么向量
与向量
的夹角为
A．
B．
C．
D．
3．
的展开式中第三项的系数是
A．
B．
C．15 D．
4．圆
与直线
相切于点
，则直线的方程为
A．
B．
C．
D．
. | x |
在刚刚结束的全国第七届全国农运会期间，某体育场馆橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品，其中第1堆只有1层，就一个球；第
堆最底层（第一层）分别按图1所示方式固定摆放，从第二层开始，每层的小球自然垒放在下一层之上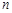，第
堆第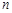层就放一个乒乓球，以
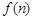表示这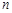堆的乒乓球总数，则
；
（
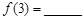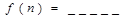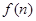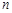的答案用表示）
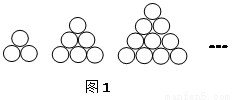
和方差s2，并根据计算结果估计哪位运动员的成绩比较稳定．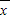
和方差s2，并根据计算结果估计哪位运动员的成绩比较稳定．一、选择题：
1．C．提示：
．
2．A．提示：直接利用“更相减损术”原理逐步运算即可.
3．B．提示：
为实数，所以
．
４．Ｃ．提示：这是一个条件分支结构，实质是分段函数求最值问题，将函数定义域分为三段讨论即可求解.分段函数为：
，
当
时，解得
，不合题意；当
时，解得
，不合题意；
当
时，解得
，符合题意，所以当输入
的值为３时，输出
的值为８.
５．B.提示：由
为纯虚数得：
．由
，解得：
.因为
为第四象限角，所以
，则
，选B.
６．Ｃ．提示：此算法的功能为求解
当
取到第一个大于或等于
的值时，的表达式中最后一项的值．
由
．所以
时，
．
此时
．
７．C．提示：令
，则
，∴
．
８．D．提示：框图的功能是寻找满足
的最小的自然数
，可解得，
，
所以
，则输出的值为
．
９．Ｄ．提示：
，此复数的对应点为
，因为
，所以
，所以此复数的对应点在第四象限．
10．B．提示：设工序c所需工时数为x天，由题设关键路线是a→c→e→g.需工时1+x+4+1=10.∴x=4，即工序c所需工时数为4天．
11．Ａ．提示：
，
，
……，所以
．
12．Ａ．提示：根据题意可得：
，解得
．所以点
落在以
为端点的线段上，如右图．
表示线段
上的点到
的距离之和，显然当
共线时，和最小，此时，点是直线
的交点，由图知，交点为
，所以
．
．
，当
时，
，
．
二、填空题
13．
，
．提示：这是一个当型循环结构，由条件可知判断的条件是：；处理框所填的是：．
14．21分钟．提示：根据流程，可以先烧水，泡面，在烧水泡面的11分钟里，可以同时洗脸刷牙和上网查资料，这样最短可用去11分钟，然后吃饭用10分钟，这样他做完这些事情用的最短时间为21分钟．
15．
．提示：设方程的实根为
，代入方程得
，可化为
，所以有
，解得
，
所以
，所以其共轭复数为．
16．４．提示：从图中可以看出，一件成品必须经过的工序次数是粗加工、检验、精加工或返修加工、检验，至少四次．
三、解答题：
17．解：由题知平行四边形三顶点坐标为
，
设D点的坐标为 
．
因为
，得
，
得
得
，即
，
所以
，则
对应的复数为
．
⑵因为
，所以复数
的对应点Ｚ在以
为圆心，以２为半径的圆上，
则
的最大值为
．
18．解：
19．解：因为
，
，
所以，若
，则
，
消去
可得：
，
可化为
，则当
时，
取最小值
；当
时，取最大值7．
所以
．
20．解：此程序的功能是求解函数
的函数值．
根据题意知
则当
且
时，
；当
且时，
；
所以
，可以化为
，
当时，
时，有最小值
；当时，则
时，有最小值
．
因为
，所以所得
值中的最小值为１.
21．解：
，
所以
．因为
，所以
，
所以
，则
，即的模的取值范围为
．
22．解：（1）算法的功能为：
（2）程序框图为：
⑶程序语句为：
；
；
；
；
w.w.w.k.s.5.u.c.o.m
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com