
题目列表(包括答案和解析)
 (2011•丰台区二模)已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△BC'D,使得平面BC'D⊥平面ABD.
(2011•丰台区二模)已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△BC'D,使得平面BC'D⊥平面ABD.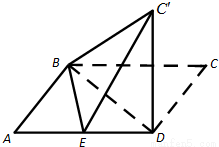
(本题满分14分) 袋中有分别写着“团团”和“圆圆”的两种玩具共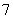 个且形状完全相同,从中任取
个且形状完全相同,从中任取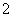 个玩具都是“圆圆”的概率为
个玩具都是“圆圆”的概率为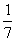 ,
,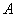 、
、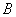 两人不放回从袋中轮流摸取一个玩具,
两人不放回从袋中轮流摸取一个玩具,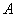 先取,
先取,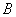 后取,然后
后取,然后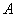 再取,……直到两人中有一人取到“圆圆”时即停止游戏.每个玩具在每一次被取出的机会是均等的,用
再取,……直到两人中有一人取到“圆圆”时即停止游戏.每个玩具在每一次被取出的机会是均等的,用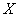 表示游戏终止时取玩具的次数.
表示游戏终止时取玩具的次数.
(1)求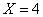 时的概率;
时的概率;
(2)求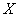 的数学期望.
的数学期望.
选修4-1:几何证明选讲
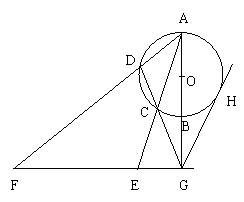 如图所示,AB是⊙O的直径,
如图所示,AB是⊙O的直径,
G为AB延长线上的一点,GCD是⊙O的割线,过点(
G作AB的垂线,交AC的延长线于点E,交AD的延
长线于点F,过G作⊙O的切线,切点为H .
求证:(Ⅰ)C,D,F,E四点共圆;
(Ⅱ)GH2=GE·GF.
在△ABC中, 角A, B, C所对的边分别为a, b, c, 且满足
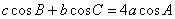 .
.
(Ⅰ) 求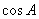 的值;
的值;
(Ⅱ) 若△ABC的面积是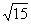 , 求
, 求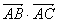 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com