
题目列表(包括答案和解析)
已知函数
(1)若函数 的图象经过P(3,4)点,求a的值;
的图象经过P(3,4)点,求a的值;
(2)比较 大小,并写出比较过程;
大小,并写出比较过程;
(3)若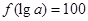 ,求a的值.
,求a的值.
【解析】本试题主要考查了指数函数的性质的运用。第一问中,因为函数 的图象经过P(3,4)点,所以
的图象经过P(3,4)点,所以 ,解得
,解得 ,因为
,因为 ,所以
,所以 .
.
(2)问中,对底数a进行分类讨论,利用单调性求解得到。
(3)中,由 知,
知, .,指对数互化得到
.,指对数互化得到 ,,所以
,,所以 ,解得所以,
,解得所以, 或
或  .
.
解:⑴∵函数 的图象经过
的图象经过 ∴
∴ ,即
,即 . … 2分
. … 2分
又 ,所以
,所以 .
………… 4分
.
………… 4分
⑵当 时,
时, ;
;
当 时,
时, . ……………… 6分
. ……………… 6分
因为, ,
,
当 时,
时, 在
在 上为增函数,∵
上为增函数,∵ ,∴
,∴ .
.
即 .当
.当 时,
时, 在
在 上为减函数,
上为减函数,
∵ ,∴
,∴ .即
.即 . …………………… 8分
. …………………… 8分
⑶由 知,
知, .所以,
.所以, (或
(或 ).
).
∴ .∴
.∴ , … 10分
, … 10分
∴ 或
或
 ,所以,
,所以, 或
或  .
.
标准正态分布的概率密度函数是P(x)=![]() ·
·![]() (x∈R).
(x∈R).
(1)求证:P(x)是偶函数;
(2)求P(x)的最大值;
(3)利用指数函数的性质说明P(x)的增减性.
莆田十中高三(1)研究性学习小组对函数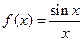 的性质进行了探究,
的性质进行了探究,
小组长收集到了以下命题:
下列说法中正确命题的序号是 .(填出所有正确命题的序号)
①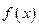 是偶函数; ②
是偶函数; ②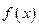 是周期函数;
是周期函数;
③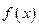 在区间(0,
在区间(0,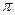 )上的单调递减; ④
)上的单调递减; ④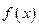 没有值最大值.
没有值最大值.
某学生对函数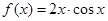 的性质进行研究,得出如下的结论:
的性质进行研究,得出如下的结论:
①函数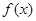 在
在 上单调递增,在
上单调递增,在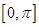 上单调递减;
上单调递减;
②点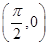 是函数
是函数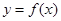 图像的一个对称中心;
图像的一个对称中心;
③函数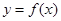 图像关于直线
图像关于直线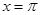 对称;
对称;
④存在常数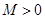 ,使
,使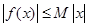 对一切实数
对一切实数 均成立.其中正确的结论是
.
均成立.其中正确的结论是
.
莆田十中高三(1)研究性学习小组对函数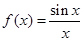 的性质进行了探究,
的性质进行了探究,
小组长收集到了以下命题:
下列说法中正确命题的序号是 .(填出所有正确命题的序号)
①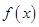 是偶函数;
②
是偶函数;
②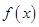 是周期函数;
是周期函数;
③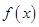 在区间(0,
在区间(0,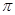 )上的单调递减; ④
)上的单调递减; ④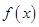 没有值最大值.
没有值最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com