
题目列表(包括答案和解析)
在数列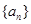 中,
中,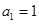 ,当
,当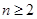 时,
时,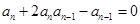
(Ⅰ)求数列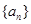 的通项公式;
的通项公式;
(Ⅱ)设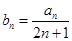 ,求数列
,求数列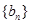 的前
的前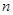 项和
项和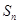 .
.
【解析】本试题主要考查了数列的通项公式的求和 综合运用。第一问中 ,利用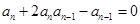 ,得到
,得到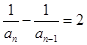 且
且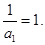 ,故故
,故故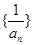 为以1为首项,公差为2的等差数列. 从而
为以1为首项,公差为2的等差数列. 从而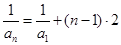

第二问中,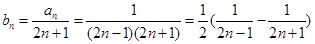
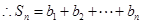
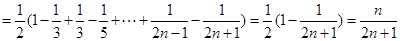
由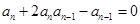 及
及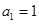 知
知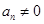 ,从而可得
,从而可得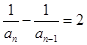 且
且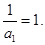
故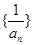 为以1为首项,公差为2的等差数列.
为以1为首项,公差为2的等差数列.
从而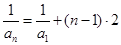
 ……………………6分
……………………6分
(2)
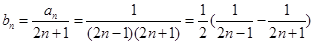 ……………………9分
……………………9分
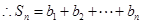
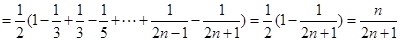
已知函数![]() ,
,![]() 。
。
(I)当函数![]() 取得最大值时,求自变量
取得最大值时,求自变量![]() 的集合;
的集合;
(II)该函数的图象可由![]() 的图象经过怎样的平移和伸缩变换
的图象经过怎样的平移和伸缩变换
得到?
已知指数函数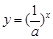 ,当
,当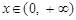 时,有
时,有 ,解关于x的不等式
,解关于x的不等式
【解析】本试题主要考查了指数函数,对数函数性质的运用。首先利用指数函数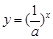 ,当
,当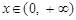 时,有
时,有 ,,得到
,,得到 ,从而
,从而
 等价于
等价于 ,联立不等式组可以解得
,联立不等式组可以解得
解:∵ 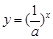 在
在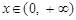 时,有
时,有 ,
∴
,
∴  。
。
于是由 ,得
,得 ,
,
解得 ,
∴ 不等式的解集为
,
∴ 不等式的解集为 。
。
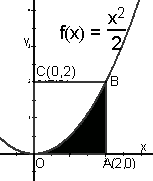
如右上图示,利用随机模拟的方法可以估计图中由曲线![]() 所围成的阴影部分的面积S:(1)先产生两组0~1的均匀随机数,a=RAND(),b=RAND();
所围成的阴影部分的面积S:(1)先产生两组0~1的均匀随机数,a=RAND(),b=RAND();
(2)做变换,令x=2a, y=2b;(3)产生N个点(x,y),并统计满足条件![]() 的点(x, y)的个数
的点(x, y)的个数![]()
![]() .已知某同学用计算器做模拟试验结果当N=1000时
.已知某同学用计算器做模拟试验结果当N=1000时![]() =332,则据此可估计S=_________ 。
=332,则据此可估计S=_________ 。
 |
已知向量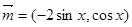 ,
,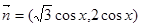 ,函数
,函数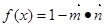 ,
,
(1)求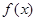 的最小正周期;
的最小正周期;
(2)当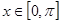 时,求
时,求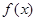 的单调递增区间;
的单调递增区间;
(3)说明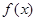 的图像可以由
的图像可以由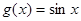 的图像经过怎样的变换而得到。
的图像经过怎样的变换而得到。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com