题目列表(包括答案和解析)
| π |
| 4 |
| π |
| 8 |
| kπ |
| 2 |
|
| π |
| 8 |
| kπ |
| 2 |
|
| 3 |
| 1 |
| 3 |
| 1 |
| 6 |
| 21 |
| 4 |
| 23 |
| 4 |
时，f（x）取得最大值2．
）的单调递增区间，并指出该函数的图象可以由函数y=2sinx，x∈R的图象经过怎样的变换得到？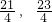
]上是否存在f（x）的对称轴？如果存在，求出其对称轴方程；如果不存在，则说明理由．| 1 |
| 3 |
| 1 |
| 6 |
| 21 |
| 4 |
| 23 |
| 4 |
一、选择题(每小题5分，共50分)
1．B 2．C 3．A 4．D 5．C 6．D 7．B 8．C 9．A 10．D
二、填空题（每小题4分，共24分）
11．180 12．60 13．
14．2 15．5 16．
三、解答题(本大题共6小题，共76分)
17．(本题12分)
解：（Ⅰ）
………………………………（2分）
…………（4分）
…………………………………(6分)
(Ⅱ)
． ……………(8分)
由已知条件
根据正弦定理，得
…………………（10分）
……………………（12分）
18．（本题12分）
解：（Ⅰ）
……………………（2分）
……………………（4分）
……………………（6分）
当
时，有
(人)．
在的基础上，
有
(人)，
……………………（8分）
(Ⅱ)
…………（10分）
…………………………………（12分）
19．(本题12分)
证明：(Ⅰ)
在△
中，
…………………………（2分）
平面
．
…………………………（4分）
平面
…………………………（6分）
(Ⅱ)连接
交
于M，则M为的中点 …………………………（8分）
连接DM，则
∥
，
…………………………（10分）
平面
，
平面，
∥平面
…………………………（12分）
20．（本题12分）
解：(Ⅰ)由已知得
，又
，
即
． …………………………（2分）
，公差
．
由
，得 …………………………（4分）
即
．解得
或
(舍去)．
．
…………………………（6分）
(Ⅱ)由
得
…………………………（8分）
…………………………（9分）
是等差数列．
则
………………………(11分)
……………………(12分)
21．(本题14分)
解：(Ⅰ)依题意得
．
………………………（2分）
把（1，3）代入．
解得
．
椭圆的方程为
．
………………………（4分）
(Ⅱ)由(Ⅰ)得
，设
，如图所示
点在椭圆上，
． ①
点异于顶点
、
，
．
由
、、三点共线，可得
从而
…………………………（7分）
② …………（8分）
将①式代入②式化简得
…………（10分）
…………（12分）
于是
为锐角，
为钝角． ……………(14分)
22．(本题14分)
解：（Ⅰ）
，
令
，得
或
．
………………（2分）
当
时，
在
上单调递增；
当
时，
在
上单调递减，
而
，
当
时，
的值域是
． ……………（4分）(Ⅱ)设函数
在
上的值域是A，
若对任意
．总存在
1,使
，
．
……………（6分）
．
①当
时，
，
函数在
上单调递减．
，
当时，不满足
； ……………………(8分)
②当
时，
，
令
，得
或
(舍去 ………………(9分)
（i）
时，
的变化如下表：
0
2
-
0
+
0
．
，解得
． …………………(11分)
(ii)当
时，
函数在上单调递减．
，当时，不满足．
…………………(13分)
综上可知，实数
的取值范围是
． ……………………（14分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com