练习册

  • 练习册
  • 试题
    ①-②得: 所以,所求通项为----5分 【查看更多】

     

    题目列表(包括答案和解析)

    已知正项数列的前n项和满足：，

    （1）求数列的通项和前n项和；

    （2）求数列的前n项和；

    （3）证明：不等式  对任意的，都成立．

    【解析】第一问中，由于所以

    两式作差，然后得到

    从而得到结论

    第二问中，利用裂项求和的思想得到结论。

    第三问中，

    又

           

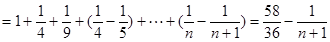
    结合放缩法得到。

    解：（1）∵     ∴

          ∴

          ∴   ∴  ………2分

          又∵正项数列，∴           ∴ 

    又n=1时，

    ∴   ∴数列是以1为首项，2为公差的等差数列……………3分

    ∴                             …………………4分

    ∴                   …………………5分 

    （2）       …………………6分

        ∴

                              …………………9分

    （3）

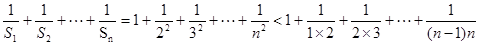
          …………………12分

    又

            ，

       ∴不等式  对任意的，都成立．

     

    查看答案和解析>>

    对于数列{An}：A1，A2，A3，…，An，若不改变A1，仅改变A2，A3，…，An中部分项的符号，得到的新数列{an}称为数列{An}的一个生成数列．如仅改变数列1，2，3，4，5的第二、三项的符号可以得到一个生成数列1，-2，-3，4，5．已知数列{an}为数列{
    1
    2n
    }(n∈N*)    的生成数列，Sn为数列{an}的前n项和．
    （1）写出S3的所有可能值；
    （2）若生成数列{an}的通项公式为an=
    1
    2n
    ，n=3k+1
    -
    1
    2n
    ，n≠3k+1
    ，k∈N    ，求Sn；
    （3）用数学归纳法证明：对于给定的n∈N*，Sn的所有可能值组成的集合为：{x|x=
    2m-1
    2n
    ，m∈N*，m≤2n-1}    ．

    查看答案和解析>>

    对于数列{An}：A1，A2，A3，…，An，若不改变A1，仅改变A2，A3，…，An中部分项的符号，得到的新数列{an}称为数列{An}的一个生成数列．如仅改变数列1，2，3，4，5的第二、三项的符号可以得到一个生成数列1，-2，-3，4，5．已知数列{an}为数列{
    1
    2n
    }(n∈N*)    的生成数列，Sn为数列{an}的前n项和．
    （1）写出S3的所有可能值；
    （2）若生成数列{an}的通项公式为an=
    1
    2n
    ，n=3k+1
    -
    1
    2n
    ，n≠3k+1
    ，k∈N    ，求Sn；
    （3）用数学归纳法证明：对于给定的n∈N*，Sn的所有可能值组成的集合为：{x|x=
    2m-1
    2n
    ，m∈N*，m≤2n-1}    ．

    查看答案和解析>>

    对于数列{An}：A1，A2，A3，…，An，若不改变A1，仅改变A2，A3，…，An中部分项的符号，得到的新数列{an}称为数列{An}的一个生成数列．如仅改变数列1，2，3，4，5的第二、三项的符号可以得到一个生成数列1，-2，-3，4，5．已知数列{an}为数列{
    1
    2n
    }(n∈N*)    的生成数列，Sn为数列{an}的前n项和．
    （1）写出S3的所有可能值；
    （2）若生成数列{an}满足：S3n=
    1
    7
    (1-
    1
    8n
    )    ，求{an}的通项公式；
    （3）证明：对于给定的n∈N*，Sn的所有可能值组成的集合为：{x|x=
    2m-1
    2n
    ，m∈N*，m≤2n-1}    ．

    查看答案和解析>>

    2007年12月29日第十届全国人大常委会第三十一次会议表决通过了《关于修改〈中华人民共和国个人所得税法〉的决定》，将个人所得税工资、薪金所得减除费用标准由每月1600元提高到每月2000元，同时明确自2008年3月1日起施行．即公民全月工资，薪金所得不超过2000元的部分不必纳税，超过2000元的部分应纳税，此项税款按下表分段累进计算：

    注明：上表中“全月应纳税所得额”是从月工资、薪金收入中减去2000元后的余额．例如某人月工资、薪金收入为3000元，减去2000元，应纳税所得额为1000元，由税率表知其中500元税率为5％，另外500元的税率为10％，所以此人应纳个人所得税为500×5％＋500×10％＝75元．

    (1)请写出月工资，薪金的个人所得税y关于工资，薪金收入x(0＜x≤5000)的函数表达式；

    (2)某高中数学教师在2008年10月份缴纳的个人所得税是40元，试求他这个月的工资，薪金收入是多少？

    查看答案和解析>>


    同步练习册答案