
题目列表(包括答案和解析)
①存在平面![]() ,使得α、β都垂直于
,使得α、β都垂直于![]() ;
;
②存在平面![]() ,使得α、β都平等于
,使得α、β都平等于![]() ;
;
③存在直线![]() ,直线
,直线![]() ,使得
,使得![]() ;
;
④存在异面直线l、m,使得![]()
其中,可以判定α与β平行的条件有( )
A.1个 B.2个 C.3 D.4个
对于不重合的两个平面 ,给定下列条件:
,给定下列条件:
①存在直线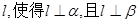 ;
;
②存在平面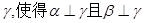 ;
;
③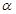 内有不共线的三点到
内有不共线的三点到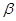 的距离相等;
的距离相等;
④存在异面直线
其中,可以判定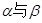 平行的条件有 (
)
平行的条件有 (
)
A.1个 B.2个 C.3个 D.4个
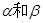 ,给定下列条件:
,给定下列条件: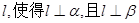 ;
; 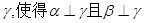 ;
;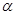 内有不共线的三点到
内有不共线的三点到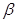 的距离相等;
的距离相等; 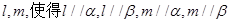
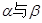 平行的条件有 ( )
平行的条件有 ( )| A.1个 | B.2个 | C.3个 | D.4个 |
对于不重合的两个平面α,β,给定下列条件:
①存在直线l,使l⊥α,l⊥β;
②存在平面γ,使α⊥γ,β⊥γ;
③α内有不共线三点到β的距离相等;
④存在异面直线l,m,使l∥α,l⊥β,m∥α,m∥β.
其中可以判定α∥β的有________个.
A.0
B.1
C.2
D.3
对于不重合的两个平面α,β,给定下列条件:
①存在直线l,使l⊥α,l⊥β;
②存在平面γ,使α⊥γ,β⊥γ;
③α内有不共线三点到β的距离相等;
④存在异面直线l,m,使l∥α,l∥β,m∥α,m∥β.
其中可以判定α∥β的有________个
A.1
B.2
C.3
D.4
一、ADBAB CDCBC
二、11 9 12  13 384 14
13 384 14  15
15 

三、解答题
16.解:(I)
又 ,∴
,∴ ,
, ……5分
……5分
(II)

17.解:(Ⅰ) 抛掷一次出现的点数共有6×6 = 36种不同结果,其中“点数之和为
∴抛掷一次出现的点数之和为7的概率为 ………………………… 2分
………………………… 2分
ξ可取1 , 2 , 3 , 4
P (ξ=1) = ,P (ξ=2) =
,P (ξ=2) = ,P (ξ= 3) =
,P (ξ= 3) =
P (ξ= 4) =
∴ξ的概率分布列为
ξ
1
2
3
4
P



|