
题目列表(包括答案和解析)
(本题满分12分)A、B两城相距100 km,在两地之间距A城x (km)处建一核电站给A、B两城供电,为保证城市安全,核电站距城市距离不得少于10km。已知供电费用等于供电距离(km)的平方与供电量(亿度)之积的0.25倍,若A城供电量为每月20亿度,B城为每月10亿度。
(1)求x的取值范围;(2)把月供电总费用y表示成x的函数; (3)核电站建在距A城多远,才能使供电总费用y最小。
(本题满分12分)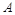 、
、 两城相距100km,在两地之间 (直线AB上)距
两城相距100km,在两地之间 (直线AB上)距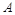 城
城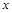 km处的
km处的 地建一核电站给
地建一核电站给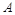 、
、 两城供电,为保证城市安全,核电站与城市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数为0.3,若
两城供电,为保证城市安全,核电站与城市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数为0.3,若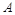 城供电量为20亿度/月,
城供电量为20亿度/月, 城为10亿度/月.
城为10亿度/月.
(1)求月供电总费用 表示成
表示成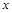 的函数;
的函数;
(2)核电站建在距A城多远,才能使供电费用最小?
(本题满分12分)围建一个面积为360㎡的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修),其它三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2m的进出口,如图所示。已知旧墙的维修费用为45元/m ,新墙的造价为180元/m ,设利用的旧墙的长度为 (单位:m), 修建此矩形场地围墙的总费用为
(单位:m), 修建此矩形场地围墙的总费用为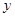 (单位:元)。
(单位:元)。
(1)将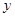 表示为
表示为 的函数;
的函数;
(2)试确定 ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。

(本题满分12分)![]() 、
、![]() 两城相距100km,在两地之间 (直线AB上)距
两城相距100km,在两地之间 (直线AB上)距![]() 城
城![]() km处的
km处的![]() 地建一核电站给
地建一核电站给![]() 、
、![]() 两城供电,为保证城市安全,核电站与城市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数为0.3,若
两城供电,为保证城市安全,核电站与城市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数为0.3,若![]() 城供电量为20亿度/月,
城供电量为20亿度/月,![]() 城为10亿度/月.
城为10亿度/月.
(1)求月供电总费用![]() 表示成
表示成![]() 的函数;
的函数;
(2)核电站建在距A城多远,才能使供电费用最小?
(本题满分12分)
A、B两城相距100 km,在两地之间距A城x (km)处建一核电站给A、B两城供电,为保证城市安全,核电站距城市距离不得少于10km。已知供电费用等于供电距离(km)的平方与供电量(亿度)之积的0.25倍,若A城供电量为每月20亿度,B城为每月10亿度。
(1)求x的取值范围;
(2)把月供电总费用y表示成x的函数;
(3)核电站建在距A城多远,才能使供电总费用y最小。
一、ADBAB CDCBC
二、11 9 12  13 384 14
13 384 14  15
15 

三、解答题
16.解:(I)
又 ,∴
,∴ ,
, ……5分
……5分
(II)

17.解:(Ⅰ) 抛掷一次出现的点数共有6×6 = 36种不同结果,其中“点数之和为
∴抛掷一次出现的点数之和为7的概率为 ………………………… 2分
………………………… 2分
ξ可取1 , 2 , 3 , 4
P (ξ=1) = ,P (ξ=2) =
,P (ξ=2) = ,P (ξ= 3) =
,P (ξ= 3) =
P (ξ= 4) =
∴ξ的概率分布列为
ξ
1
2
3
4
P



|