
题目列表(包括答案和解析)
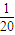 相切,且与圆x2+(y-
相切,且与圆x2+(y- )2=
)2=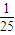 外切.
外切. +
+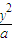 =1(0<a<2).已知直线L与抛物线C交于A、B两个不同点,L与椭圆E交于P、Q两个不同点,设AB中点为R,PQ中点为S,若
=1(0<a<2).已知直线L与抛物线C交于A、B两个不同点,L与椭圆E交于P、Q两个不同点,设AB中点为R,PQ中点为S,若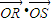 =0,求E离心率的范围.
=0,求E离心率的范围.已知以点C (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M、N,若|OM|=|ON|,求圆C的方程;
(3)在(2)的条件下,设P、Q分别是直线l:x+y+2=0和圆C的动点,求|PB|+|PQ|的最小值及此时点P的坐标.
已知以点C (t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M,N,若|OM|=|ON|,求圆C的方程;
(3)在(2)的条件下,设P,Q分别是直线l:x+y+2=0和圆C上的动点,求|PB|+|PQ|的最小值及此时点P的坐标.
已知以点C (t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M,N,若|OM|=|ON|,求圆C的方程;
(3)在(2)的条件下,设P,Q分别是直线l:x+y+2=0和圆C上的动点,求|PB|+|PQ|的最小值及此时点P的坐标..
已知以点C (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M、N,若|OM|=|ON|,求圆C的方程;
(3)在(2)的条件下,设P、Q分别是直线l:x+y+2=0和圆C的动点,求|PB|+|PQ|的最小值及此时点P的坐标.
难点磁场
证明:设线段的方程为y=f(x)=(bc-1)x+2-b-c,其中|b|<1,|c|<1,|x|<1,且-1<b<1.
∵f(-1)=1-bc+2-b-c=(1-bc)+(1-b)+(1-c)>0
f(1)=bc-1+2-b-c=(1-b)(1-c)>0
∴线段y=(bc-1)x+2-b-c(-1<x<1)在x轴上方,这就是说,当|a|<1,|b|<1,|c|<1时,恒有abc+2>a+b+c.
歼灭难点训练
一、1.解析:将问题转化为比较A(-1,-1)与B(102001,102000)及C(102002,102001)连线的斜率大小,因为B、C两点的直线方程为y= x,点A在直线的下方,∴kAB>kAC,即M>N.
x,点A在直线的下方,∴kAB>kAC,即M>N.
答案:A
2.解析:设三角形的另外两边长为x,y,则
当x=1时,y=11;当x=2时,y=10,11;
当x=3时,y=9,10,11;当x=4时,y=8,9,10,11;
当x=5时,y=7,8,9,10,11.
以上共有15个,x,y对调又有15个,再加上(6,6),(7,7),(8,8),(9,9),(10,10)、(11,11)六组,所以共有36个.
答案:C
二、3.解析:找A关于l的对称点A′,A′B与直线l的交点即为所求的P点.
答案:P(5,6)
4.解析:光线l所在的直线与圆x2+y2-4x-4y+7=0关于x轴对称的圆相切.
答案:3x+4y-3=0或4x+3y+3=0
5.解析:f(θ)= 表示两点(cosθ,sinθ)与(2,1)连线的斜率.
表示两点(cosθ,sinθ)与(2,1)连线的斜率.
6.解析:原不等式变为(x2-1)m+(1-2x)<0,构造线段f(m)=(x2-1)m+1-2x,-2≤m≤2,则f(-2)<0,且f(2)<0.
三、7.(1)证明:设A、B的横坐标分别为x1、x2,由题设知x1>1,x2>1,?
点A(x1,log8x1),B(x2,log8x2).
因为A、B在过点O的直线上,所以 ,又点C、D的坐标分别为(x1,log2x1)、(x2,log2x2).
,又点C、D的坐标分别为(x1,log2x1)、(x2,log2x2).
由于log2x1=3log8x1,log2x2=3log8x2,则
由此得kOC=kOD,即O、C、D在同一直线上.
(2)解:由BC平行于x轴,有log2x1=log8x2,又log2x1=3log8x1
∴x2=x13
由于x1>1知log8x1≠0,故x13=3x1x2= ,于是A(
,于是A( ,log8
,log8 ).
).
9.(1)证明:由条件,得a1=S1=a,当n≥2时,
有an=Sn-Sn-1=[na+n(n-1)b]-[(n-1)a+(n-1)(n-2)b]=a+2(n-1)b.
因此,当n≥2时,有an-an-1=[a+2(n-1)b]-[a+2(n-2)b]=2b.
所以{an}是以a为首项,2b为公差的等差数列.
∴所有的点Pn(an, -1)(n=1,2,…)都落在通过P1(a,a-1)且以
-1)(n=1,2,…)都落在通过P1(a,a-1)且以 为斜率的直线上.此直线方程为y-(a-1)=
为斜率的直线上.此直线方程为y-(a-1)=  (x-a),即x-2y+a-2=0.
(x-a),即x-2y+a-2=0.
(3)解:当a=1,b= 时,Pn的坐标为(n,
时,Pn的坐标为(n, ),使P1(1,0)、P2(2,
),使P1(1,0)、P2(2,  )、P3(3,1)都落在圆C外的条件是
)、P3(3,1)都落在圆C外的条件是
由不等式①,得r≠1
故使P1、P2、P3都落在圆C外时,r的取值范围是(0,1)∪(1, -
- )∪(4+
)∪(4+ ,+∞).
,+∞).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com