
题目列表(包括答案和解析)
设A、B是椭圆 上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
(Ⅰ)确定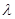 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;
(Ⅱ)当 时求由A、B、C、D四点组成的四边形的面积。
时求由A、B、C、D四点组成的四边形的面积。
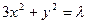 上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.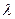 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程; 时求由A、B、C、D四点组成的四边形的面积。
时求由A、B、C、D四点组成的四边形的面积。已知直线 :
: (k
(k R)与圆C:
R)与圆C: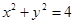 相交于点A、B, M为弦AB中点.
相交于点A、B, M为弦AB中点.
(Ⅰ) 当k=1时,求弦AB的中点M的坐标及AB弦长;
(Ⅱ)求证:直线 与圆C总有两个交点;
与圆C总有两个交点;
(Ⅲ)当k变化时求弦AB的中点M的轨迹方程.
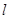 :
: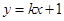 (k
(k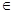 R)与圆C:
R)与圆C: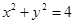 相交于点A、B, M为弦AB中点.
相交于点A、B, M为弦AB中点.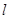 与圆C总有两个交点;
与圆C总有两个交点;若直线y=x+t与椭圆![]() 相交于A、B两点,当t变化时,|AB|的最大值是( )
相交于A、B两点,当t变化时,|AB|的最大值是( )
A、2 B、![]() C、
C、![]() D、
D、![]()
一、选择题:
CADCB AABBD CD
二、填空题
(13)解析几何测试题(文科).files/image262.gif) ; (14)8; (15)
; (14)8; (15)解析几何测试题(文科).files/image264.gif) ; (16)3.
; (16)3.
三、解答题
(17)解:将圆C的方程解析几何测试题(文科).files/image172.gif) 配方得标准方程为
配方得标准方程为解析几何测试题(文科).files/image266.gif) ,
,
则此圆的圆心为(0 , 4),半径为2.
(Ⅰ) 若直线解析几何测试题(文科).files/image144.gif) 与圆C相切,则有
与圆C相切,则有解析几何测试题(文科).files/image268.gif) . 解得
. 解得解析几何测试题(文科).files/image270.gif) . ………………6分
. ………………6分
(Ⅱ) 解:过圆心C作CD⊥AB,则根据题意和圆的性质,得
解析几何测试题(文科).files/image272.gif) 解得
解得解析几何测试题(文科).files/image274.gif) .
.
∴直线解析几何测试题(文科).files/image144.gif) 的方程是
的方程是解析几何测试题(文科).files/image276.gif) 和
和解析几何测试题(文科).files/image278.gif) . ………………12分
. ………………12分
(18)解:(Ⅰ)由题意知此平面区域表示的是以解析几何测试题(文科).files/image280.gif) 构成的三角形及其内部,且△
构成的三角形及其内部,且△解析几何测试题(文科).files/image282.gif) 是直角三角形, 所以覆盖它的且面积最小的圆是其外接圆,故圆心是(2,1),半径是
是直角三角形, 所以覆盖它的且面积最小的圆是其外接圆,故圆心是(2,1),半径是解析几何测试题(文科).files/image284.gif) ,
,
所以圆解析几何测试题(文科).files/image183.gif) 的方程是
的方程是解析几何测试题(文科).files/image287.gif) . ………………6分
. ………………6分
(Ⅱ)设直线解析几何测试题(文科).files/image144.gif) 的方程是:
的方程是:解析几何测试题(文科).files/image289.gif) .
.
因为解析几何测试题(文科).files/image291.gif) ,所以圆心
,所以圆心解析几何测试题(文科).files/image183.gif) 到直线
到直线解析几何测试题(文科).files/image144.gif) 的距离是
的距离是解析几何测试题(文科).files/image293.gif) , 即
, 即解析几何测试题(文科).files/image295.gif) .
.
解得:解析几何测试题(文科).files/image297.gif) . ………………………………11分
. ………………………………11分
所以直线解析几何测试题(文科).files/image144.gif) 的方程是
的方程是解析几何测试题(文科).files/image299.gif) . ………………12分
. ………………12分
(19)解:设过点T(3,0)的直线解析几何测试题(文科).files/image191.gif) 交抛物线
交抛物线解析几何测试题(文科).files/image301.gif) 于点A
于点A解析几何测试题(文科).files/image303.gif) 、B
、B解析几何测试题(文科).files/image305.gif) .
.
(Ⅰ)当直线解析几何测试题(文科).files/image191.gif) 的钭率不存在时,直线
的钭率不存在时,直线解析几何测试题(文科).files/image191.gif) 的方程为
的方程为解析几何测试题(文科).files/image307.gif) ,
,
此时, 直线解析几何测试题(文科).files/image191.gif) 与抛物线相交于点A(3,
与抛物线相交于点A(3,解析几何测试题(文科).files/image309.gif) )().B(3,-
)().B(3,-解析几何测试题(文科).files/image309.gif) ),∴
),∴解析几何测试题(文科).files/image312.gif) =3. …….............4分
=3. …….............4分
(Ⅱ)当直线解析几何测试题(文科).files/image191.gif) 的钭率存在时,设直线
的钭率存在时,设直线解析几何测试题(文科).files/image191.gif) 的方程为
的方程为解析几何测试题(文科).files/image314.gif) ,
,
其中解析几何测试题(文科).files/image316.gif) ,由
,由解析几何测试题(文科).files/image318.gif) 得
得 解析几何测试题(文科).files/image320.gif) .
…………………….….6分
.
…………………….….6分
又 ∵ 解析几何测试题(文科).files/image322.gif) , ∴
, ∴解析几何测试题(文科).files/image324.gif) ,
,
………………………………….10分
综上所述,命题“若直线解析几何测试题(文科).files/image191.gif) 过点T(3,0),则
过点T(3,0),则解析几何测试题(文科).files/image312.gif) =3” 是真命题. ………………….12分
=3” 是真命题. ………………….12分
(20)解:(Ⅰ)由解析几何测试题(文科).files/image205.gif) 知
知解析几何测试题(文科).files/image203.gif) 是
是解析几何测试题(文科).files/image328.gif) 的中点,
的中点,
设A、B两点的坐标分别为解析几何测试题(文科).files/image330.gif)
由解析几何测试题(文科).files/image332.gif) .
.
解析几何测试题(文科).files/image334.gif) ,
,
∴解析几何测试题(文科).files/image203.gif) 点的坐标为
点的坐标为解析几何测试题(文科).files/image336.gif) .
…………………………4分
.
…………………………4分
又解析几何测试题(文科).files/image203.gif) 点在直线
点在直线解析几何测试题(文科).files/image144.gif) 上,
上, 解析几何测试题(文科).files/image339.gif) .
.
解析几何测试题(文科).files/image341.gif) ,
, 解析几何测试题(文科).files/image343.gif) ………………6分
………………6分
(Ⅱ)由(Ⅰ)知解析几何测试题(文科).files/image345.gif) ,不妨设椭圆的一个焦点坐标为
,不妨设椭圆的一个焦点坐标为解析几何测试题(文科).files/image347.gif) ,
,
设解析几何测试题(文科).files/image347.gif) 关于直线
关于直线解析几何测试题(文科).files/image144.gif)
解析几何测试题(文科).files/image351.gif) 上的对称点为
上的对称点为解析几何测试题(文科).files/image353.gif) ,
,
则有解析几何测试题(文科).files/image355.gif) . ………………10分
. ………………10分
由已知解析几何测试题(文科).files/image357.gif) .
.
解析几何测试题(文科).files/image359.gif) ,∴所求的椭圆的方程为
,∴所求的椭圆的方程为解析几何测试题(文科).files/image361.gif) . ………………12分
. ………………12分
(21)解:(Ⅰ)由已知条件,直线解析几何测试题(文科).files/image144.gif) 的方程为
的方程为解析几何测试题(文科).files/image364.gif) ,
,
代入椭圆方程得解析几何测试题(文科).files/image366.gif) .
.
整理得解析几何测试题(文科).files/image368.gif) ① ……………………………………3分
① ……………………………………3分
直线解析几何测试题(文科).files/image144.gif) 与椭圆有两个不同的交点
与椭圆有两个不同的交点解析几何测试题(文科).files/image221.gif) 和
和解析几何测试题(文科).files/image223.gif) 等价于
等价于解析几何测试题(文科).files/image373.gif) ,
,
解得解析几何测试题(文科).files/image375.gif) 或
或解析几何测试题(文科).files/image377.gif) .即
.即解析几何测试题(文科).files/image216.gif) 的取值范围为
的取值范围为解析几何测试题(文科).files/image380.gif) .………………6分
.………………6分
(Ⅱ)设解析几何测试题(文科).files/image382.gif) ,则
,则解析几何测试题(文科).files/image384.gif) ,
,
由方程①,解析几何测试题(文科).files/image386.gif) . ②
. ②
又解析几何测试题(文科).files/image388.gif) . ③ …………………………………9分
. ③ …………………………………9分
而解析几何测试题(文科).files/image390.gif) .
.
所以解析几何测试题(文科).files/image231.gif) 与
与解析几何测试题(文科).files/image233.gif) 共线等价于
共线等价于解析几何测试题(文科).files/image394.gif) ,
,
将②③代入上式,解得解析几何测试题(文科).files/image396.gif) .
.
由(Ⅰ)知解析几何测试题(文科).files/image375.gif) 或
或解析几何测试题(文科).files/image377.gif) ,故没有符合题意的常数
,故没有符合题意的常数解析几何测试题(文科).files/image216.gif) .………………12分
.………………12分
解析几何测试题(文科).files/image400.gif) (22)解:(Ⅰ)设点
(22)解:(Ⅰ)设点解析几何测试题(文科).files/image402.gif) ,则
,则解析几何测试题(文科).files/image404.gif) ,由
,由解析几何测试题(文科).files/image406.gif) 得:
得:
解析几何测试题(文科).files/image408.gif) ,化简得
,化简得解析几何测试题(文科).files/image410.gif) .……4分
.……4分
(Ⅱ)(1)设直线解析几何测试题(文科).files/image328.gif) 的方程为:
的方程为:
解析几何测试题(文科).files/image413.gif) .
.
设解析几何测试题(文科).files/image415.gif) ,
,解析几何测试题(文科).files/image417.gif) ,又
,又解析几何测试题(文科).files/image419.gif)
联立方程组解析几何测试题(文科).files/image421.gif) ,消去
,消去解析几何测试题(文科).files/image006.gif) 得:
得:解析几何测试题(文科).files/image424.gif) ,
,解析几何测试题(文科).files/image426.gif) ,
,
解析几何测试题(文科).files/image428.gif) ……………………………………………7分
……………………………………………7分
由解析几何测试题(文科).files/image254.gif) ,
,解析几何测试题(文科).files/image256.gif) 得:
得:
解析几何测试题(文科).files/image432.gif) ,
,解析几何测试题(文科).files/image434.gif) ,整理得:
,整理得:解析几何测试题(文科).files/image436.gif) ,
,解析几何测试题(文科).files/image438.gif) ,
,
解析几何测试题(文科).files/image440.gif)
解析几何测试题(文科).files/image442.gif)
解析几何测试题(文科).files/image444.gif)
解析几何测试题(文科).files/image446.gif) .……10分
.……10分
(2)解: 解析几何测试题(文科).files/image448.gif)
解析几何测试题(文科).files/image450.gif)
解析几何测试题(文科).files/image452.gif)
解析几何测试题(文科).files/image454.gif)
解析几何测试题(文科).files/image456.gif) .
.
当且仅当解析几何测试题(文科).files/image458.gif) ,即
,即解析几何测试题(文科).files/image460.gif) 时等号成立,所以
时等号成立,所以解析几何测试题(文科).files/image462.gif) 最小值为
最小值为解析几何测试题(文科).files/image464.gif) . ……14分
. ……14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com