
题目列表(包括答案和解析)
 任想一个数字记为a,再由乙猜甲刚才想的数字,把乙想的数字记为b,且
任想一个数字记为a,再由乙猜甲刚才想的数字,把乙想的数字记为b,且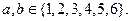
 想的数字相同或相差1,则称“甲乙心有灵犀”,求
想的数字相同或相差1,则称“甲乙心有灵犀”,求 “甲乙心有灵犀”的概率
“甲乙心有灵犀”的概率

(本小题满分12分)甲、乙两人射击,每次射击击中目标的概率分别是![]() . 现两人玩射击游戏,规则如下:若某人某次射击击中目标,则由他继续射击,否则由对方接替射击. 甲、乙两人共射击3次,且第一次由甲开始射击. 假设每人每次射击击中目标与否均互不影响.(Ⅰ)求3次射击的人依次是甲、甲、乙的概率;(Ⅱ)若射击击中目标一次得1分,否则得0分(含未射击). 用ξ表示乙的总得分,求ξ的分布列和数学期望。
. 现两人玩射击游戏,规则如下:若某人某次射击击中目标,则由他继续射击,否则由对方接替射击. 甲、乙两人共射击3次,且第一次由甲开始射击. 假设每人每次射击击中目标与否均互不影响.(Ⅰ)求3次射击的人依次是甲、甲、乙的概率;(Ⅱ)若射击击中目标一次得1分,否则得0分(含未射击). 用ξ表示乙的总得分,求ξ的分布列和数学期望。
(本小题满分12分)甲、乙两人射击,每次射击击中目标的概率分别是![]() . 现两人玩射击游戏,规则如下:若某人某次射击击中目标,则由他继续射击,否则由对方接替射击. 甲、乙两人共射击3次,且第一次由甲开始射击. 假设每人每次射击击中目标与否均互不影响.(Ⅰ)求3次射击的人依次是甲、甲、乙的概率;(Ⅱ)若射击击中目标一次得1分,否则得0分(含未射击). 用ξ表示乙的总得分,求ξ的分布列和数学期望。
. 现两人玩射击游戏,规则如下:若某人某次射击击中目标,则由他继续射击,否则由对方接替射击. 甲、乙两人共射击3次,且第一次由甲开始射击. 假设每人每次射击击中目标与否均互不影响.(Ⅰ)求3次射击的人依次是甲、甲、乙的概率;(Ⅱ)若射击击中目标一次得1分,否则得0分(含未射击). 用ξ表示乙的总得分,求ξ的分布列和数学期望。
(本小题满分12分)
甲乙两位玩家在进行“石头、剪子、布”的游戏,假设两人在游戏时出示三种手势是等可能的。
(Ⅰ)求在1次游戏中甲胜乙的概率;
(Ⅱ)若甲乙双方共进行了3次游戏,随机变量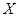 表示甲胜乙的次数,求
表示甲胜乙的次数,求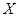 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)袋子中有质地、大小完全相同的4个球,编号分别为1,2,3,4.甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,若两个编号的和为奇数算甲赢,否则算乙赢.记基本事件为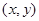 ,其中
,其中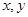 分别为甲、乙摸到的球的编号。
分别为甲、乙摸到的球的编号。
(1)列举出所有的基本事件,并求甲赢且编号的和为5的事件发生的概率;
(2)比较甲胜的概率与乙胜的概率,并说明这种游戏规则是否公平。(无详细解答过程,不给分)
(3) 如果请你猜这两球的号码之和,猜中有奖.猜什么数获奖的可能性大?说明理由.
一.选择题:BACAC DADBC
解析:
1.2009.4.files/image245.gif) ,复数
,复数 2009.4.files/image002.gif) 对应的点为
对应的点为2009.4.files/image247.gif) ,它与原点的距离是
,它与原点的距离是2009.4.files/image006.gif) ,故选B.
,故选B.
2.2009.4.files/image016.gif)
2009.4.files/image249.gif) ,但
,但2009.4.files/image018.gif)
2009.4.files/image251.gif)
2009.4.files/image016.gif) .故选A.
.故选A.
4.把直线2009.4.files/image054.gif) 向下平移二个单位,则点
向下平移二个单位,则点2009.4.files/image052.gif) 到直线
到直线2009.4.files/image253.gif) 的距离就相等了,故点
的距离就相等了,故点2009.4.files/image052.gif) 的轨迹为抛物线,它的方程为
的轨迹为抛物线,它的方程为2009.4.files/image059.gif) ,选A.
,选A.
5.依题意知,2009.4.files/image255.gif) ,
,2009.4.files/image257.gif) ,又
,又2009.4.files/image259.gif) ,
,2009.4.files/image261.gif) ,
,2009.4.files/image263.gif) ,
,2009.4.files/image265.gif) ,故选C.
,故选C.
6.当2009.4.files/image267.gif) 时,
时,2009.4.files/image085.gif) 等价于
等价于2009.4.files/image099.gif) ,当
,当2009.4.files/image269.gif) 时,
时,2009.4.files/image085.gif) 等价于
等价于2009.4.files/image097.gif) ,故选D.
,故选D.
7.∵2009.4.files/image101.gif) 是等差数列,
是等差数列,2009.4.files/image103.gif) ,
,2009.4.files/image105.gif) ,∴
,∴2009.4.files/image271.gif) ,
,2009.4.files/image273.gif) ,
,
2009.4.files/image275.gif) ∴
∴2009.4.files/image277.gif) ,故选A.
,故选A.
8.由三视图知该工作台是棱长为802009.4.files/image279.gif) 的正方体上面围上一块矩形和两块直角三角形合
的正方体上面围上一块矩形和两块直角三角形合
板,如右图示,则用去的合板的面积2009.4.files/image281.gif) 故选D.
故选D.
9.2009.4.files/image283.gif) ,
,2009.4.files/image285.gif) ,故选B.
,故选B.
2009.4.files/image287.gif) 10.由
10.由2009.4.files/image145.gif) ,可得:
,可得:2009.4.files/image290.gif) 知满足事件A的区域的面积
知满足事件A的区域的面积
2009.4.files/image292.gif) ,而满足所有条件的区域
,而满足所有条件的区域2009.4.files/image294.gif) 的面积:
的面积:2009.4.files/image296.gif) ,从而,
,从而,
得:2009.4.files/image298.gif) ,故选C.
,故选C.
二.填空题: 11. 18;12. 2009.4.files/image300.gif) ;13.
;13.2009.4.files/image302.gif) ;14.
;14. 2009.4.files/image304.gif) ;15.
;15.2009.4.files/image137.gif) 、
、2009.4.files/image135.gif) .
.
解析:11.按系统抽样的方法,样本中4位学生的座位号应成等差数列,将4位学生的座位号按从小到大排列,显然6,30不可能相邻,也就是中间插有另一位同学,其座位号为(6+30)÷2=18,故另一位同学的座位号为18.
2009.4.files/image307.gif) 12.
12.2009.4.files/image309.gif)
2009.4.files/image311.gif)
2009.4.files/image313.gif)
13.设人经过时间ts后到达点B,这时影长为AB=S,如图由平几的知识
可得2009.4.files/image315.gif) ,
,2009.4.files/image317.gif) =
=2009.4.files/image319.gif) ,由导数的意义知人影长度
,由导数的意义知人影长度
2009.4.files/image321.gif) 的变化速度v=
的变化速度v=2009.4.files/image323.gif) (m/s)
(m/s)
14.曲线2009.4.files/image161.gif) 为抛物线段
为抛物线段2009.4.files/image325.gif)
2009.4.files/image327.gif) 借助图形直观易得
借助图形直观易得2009.4.files/image304.gif)
2009.4.files/image081.gif)
15.由切割线定理得2009.4.files/image330.gif) ,
,2009.4.files/image332.gif) ,
,
连结OC,则2009.4.files/image334.gif) ,
,2009.4.files/image336.gif) ,
,2009.4.files/image338.gif)
三.解答题:
16.解:(1)2009.4.files/image171.gif)
2009.4.files/image341.gif)
2009.4.files/image343.gif) ---3分
---3分
∴函数的最小正周期为2009.4.files/image345.gif) ,值域为
,值域为2009.4.files/image347.gif) 。--------------------------------------5分
。--------------------------------------5分
(2)解法1:依题意得:2009.4.files/image349.gif)
2009.4.files/image351.gif) ---------------------------6分
---------------------------6分
∵2009.4.files/image353.gif) ∴
∴2009.4.files/image355.gif)
∴2009.4.files/image357.gif) =
=2009.4.files/image359.gif) -----------------------------------------8分
-----------------------------------------8分
2009.4.files/image178.gif) =
=2009.4.files/image361.gif)
∵2009.4.files/image363.gif) =
=2009.4.files/image365.gif)
∴2009.4.files/image178.gif) =
=2009.4.files/image367.gif) ------------------------------------------------------------------------------13分
------------------------------------------------------------------------------13分
解法2:依题意得: 2009.4.files/image351.gif) 得
得2009.4.files/image369.gif) ----①-----------7分
----①-----------7分
∵2009.4.files/image353.gif) ∴
∴2009.4.files/image355.gif)
∴2009.4.files/image357.gif) =
=2009.4.files/image359.gif) ---------------------------------9分
---------------------------------9分
由2009.4.files/image357.gif) =
=2009.4.files/image371.gif) 得
得2009.4.files/image373.gif) -----------②----------------10分
-----------②----------------10分
①+②得2009.4.files/image375.gif) ,∴
,∴2009.4.files/image178.gif) =
=2009.4.files/image367.gif) -------------------------13分
-------------------------13分
解法3:由2009.4.files/image378.gif) 得
得2009.4.files/image369.gif) ,--------------------7分
,--------------------7分
两边平方得2009.4.files/image380.gif)
2009.4.files/image382.gif) ,
,2009.4.files/image384.gif) ,--------------------------9分
,--------------------------9分
∵2009.4.files/image353.gif) ∴
∴2009.4.files/image386.gif) 由
由2009.4.files/image384.gif)
2009.4.files/image388.gif) 知
知2009.4.files/image390.gif)
∴2009.4.files/image392.gif) --------------------------------------11分
--------------------------------------11分
由2009.4.files/image394.gif) ,得
,得2009.4.files/image396.gif)
∴2009.4.files/image398.gif) ∴
∴2009.4.files/image178.gif) =
=2009.4.files/image367.gif) .---------------------------------13分
.---------------------------------13分
17.解:(1)∵2009.4.files/image182.gif) 是长方体 ∴侧面
是长方体 ∴侧面2009.4.files/image400.gif) 底面
底面2009.4.files/image402.gif)
∴四棱锥2009.4.files/image191.gif) 的高为点P到平面
的高为点P到平面2009.4.files/image402.gif) 的距离---------------------2分
的距离---------------------2分
当点P与点A重合时,四棱锥2009.4.files/image191.gif) 的高取得最大值,这时四棱锥
的高取得最大值,这时四棱锥2009.4.files/image191.gif) 体积最大----------------------------------------------------------------------------------------------------3分
体积最大----------------------------------------------------------------------------------------------------3分
在2009.4.files/image404.gif) 中∵
中∵2009.4.files/image184.gif) ∴
∴2009.4.files/image406.gif) ,------------- 4分
,------------- 4分
2009.4.files/image408.gif) ---------------------------------------------------5分
---------------------------------------------------5分
∴2009.4.files/image410.gif) -----------------------------------7分
-----------------------------------7分
(2)不论点2009.4.files/image052.gif) 在
在2009.4.files/image189.gif) 上的任何位置,都有平面
上的任何位置,都有平面2009.4.files/image193.gif) 垂直于平面
垂直于平面2009.4.files/image195.gif) .-------8分
.-------8分
证明如下:由题意知,2009.4.files/image412.gif) ,
,2009.4.files/image414.gif)
又2009.4.files/image416.gif)
2009.4.files/image418.gif) 平面
平面2009.4.files/image195.gif)
又2009.4.files/image420.gif) 平面
平面2009.4.files/image193.gif)
2009.4.files/image422.gif) 平面
平面2009.4.files/image193.gif)
2009.4.files/image169.gif) 平面
平面2009.4.files/image195.gif) .------------------- 13分
.------------------- 13分
18.解:(1)设“两个编号和为
故2009.4.files/image424.gif)
2009.4.files/image426.gif) -----------------------------------------------------------------6分
-----------------------------------------------------------------6分
(2)这种游戏规则是公平的。----------------------------------------------------------------------------7分
设甲胜为事件B,乙胜为事件C,则甲胜即两编号和为偶数所包含的基本事件数有18个:(1,1),(1,3),(1,5),(2,2),(2,4),(2,6),(3,1),(3,3),(3,5),(4,2),(4,4),(4,6),(5,1),(5,3),(5,5),(6,2),(6,4),(6,6)
所以甲胜的概率2009.4.files/image428.gif) ,乙胜的概率
,乙胜的概率2009.4.files/image430.gif) =
=2009.4.files/image432.gif) ---------------------------11分
---------------------------11分
2009.4.files/image434.gif) 所以这种游戏规则是公平的。---------------------------------------------------------------------------------12分
所以这种游戏规则是公平的。---------------------------------------------------------------------------------12分
19.解:(1)由椭圆的方程知2009.4.files/image436.gif) ,∴点
,∴点2009.4.files/image438.gif) ,
,2009.4.files/image440.gif)
2009.4.files/image081.gif) ,
,
设2009.4.files/image442.gif) 的坐标为
的坐标为2009.4.files/image444.gif) ,
,
∵FC是2009.4.files/image199.gif) 的直径,∴
的直径,∴2009.4.files/image446.gif)
∵2009.4.files/image448.gif) ∴
∴2009.4.files/image450.gif) -------------------------2分
-------------------------2分
∴2009.4.files/image452.gif) ,
,2009.4.files/image454.gif) -------------------------------------------------3分
-------------------------------------------------3分
解得2009.4.files/image456.gif) -----------------------------------------------------------------------5分
-----------------------------------------------------------------------5分
∴2009.4.files/image081.gif) 椭圆的离心率
椭圆的离心率2009.4.files/image458.gif) ---------------------------------6分
---------------------------------6分
(2)∵2009.4.files/image199.gif) 过点F,B,C三点,∴圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,FC的垂直平分线方程为
过点F,B,C三点,∴圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,FC的垂直平分线方程为2009.4.files/image460.gif) --------①-----------------------------------7分
--------①-----------------------------------7分
∵BC的中点为2009.4.files/image462.gif) ,
,2009.4.files/image464.gif)
∴BC的垂直平分线方程为2009.4.files/image466.gif) -----②---------------------9分
-----②---------------------9分
由①②得2009.4.files/image468.gif) ,即
,即2009.4.files/image470.gif) --------------------11分
--------------------11分
∵P2009.4.files/image201.gif) 在直线
在直线2009.4.files/image203.gif) 上,∴
上,∴2009.4.files/image472.gif)
2009.4.files/image474.gif)
2009.4.files/image476.gif)
∵2009.4.files/image478.gif) ∴
∴2009.4.files/image480.gif) --------------------------------------------------13分
--------------------------------------------------13分
由2009.4.files/image482.gif) 得
得2009.4.files/image484.gif)
∴椭圆的方程为2009.4.files/image486.gif) ------------------------------------------------------------------14分
------------------------------------------------------------------14分
20.解:(1)当2009.4.files/image211.gif) 时,由
时,由2009.4.files/image213.gif) 得
得2009.4.files/image488.gif) ,
,
2009.4.files/image490.gif) ;(
;(2009.4.files/image211.gif) 且
且2009.4.files/image493.gif) )------------------------------------------------------2分
)------------------------------------------------------2分
当2009.4.files/image215.gif) 时,由
时,由2009.4.files/image217.gif) .得
.得2009.4.files/image495.gif) --------------------------------------4分
--------------------------------------4分
∴2009.4.files/image497.gif) ---------------------------5分
---------------------------5分
(2)当2009.4.files/image211.gif) 且
且2009.4.files/image493.gif) 时,由
时,由2009.4.files/image500.gif) <0,解得
<0,解得2009.4.files/image502.gif) ,---------------------------6分
,---------------------------6分
当2009.4.files/image215.gif) 时,
时,2009.4.files/image505.gif) ------------------------------8分
------------------------------8分
∴函数2009.4.files/image143.gif) 的单调减区间为(-1,0)和(0,1)-----------------------------------------------9分
的单调减区间为(-1,0)和(0,1)-----------------------------------------------9分
(3)对2009.4.files/image222.gif)
2009.4.files/image224.gif) ,都有
,都有2009.4.files/image226.gif) 即
即2009.4.files/image507.gif) ,也就是
,也就是2009.4.files/image509.gif) 对
对2009.4.files/image222.gif)
2009.4.files/image224.gif) 恒成立,-------------------------------------------11分
恒成立,-------------------------------------------11分2009.4.files/image081.gif)
由(2)知当2009.4.files/image215.gif) 时,
时,2009.4.files/image511.gif)
∴函数2009.4.files/image143.gif) 在
在2009.4.files/image513.gif) 和
和2009.4.files/image515.gif) 都单调递增-----------------------------------------------12分
都单调递增-----------------------------------------------12分
又2009.4.files/image517.gif) ,
,2009.4.files/image519.gif)
当2009.4.files/image521.gif) 时
时2009.4.files/image523.gif) ,∴当
,∴当2009.4.files/image525.gif) 时,
时,2009.4.files/image527.gif)
同理可得,当2009.4.files/image529.gif) 时,有
时,有2009.4.files/image531.gif) ,
,
综上所述得,对2009.4.files/image525.gif)
2009.4.files/image224.gif) ,
, 2009.4.files/image143.gif) 取得最大值2;
取得最大值2;
∴实数2009.4.files/image022.gif) 的取值范围为
的取值范围为2009.4.files/image535.gif) .----------------------------------------------------------------14分
.----------------------------------------------------------------14分
21.解:(1)由2009.4.files/image235.gif) 得
得2009.4.files/image537.gif)
2009.4.files/image539.gif)
∴2009.4.files/image541.gif) 或
或2009.4.files/image543.gif) --------------------------------------2分
--------------------------------------2分
∵2009.4.files/image233.gif) ,∴
,∴2009.4.files/image541.gif) 不合舍去-------------------------------------------3分
不合舍去-------------------------------------------3分
由2009.4.files/image543.gif) 得
得2009.4.files/image546.gif)
方法1:由2009.4.files/image546.gif) 得
得2009.4.files/image548.gif)
∴数列2009.4.files/image237.gif) 是首项为
是首项为2009.4.files/image551.gif) ,公比为
,公比为2009.4.files/image553.gif) 的等比数列----------------------5分
的等比数列----------------------5分
〔方法2:由2009.4.files/image546.gif) 得
得2009.4.files/image555.gif)
当2009.4.files/image557.gif) 时
时2009.4.files/image559.gif)
∴2009.4.files/image561.gif) (
(2009.4.files/image557.gif) )
)
∴数列2009.4.files/image237.gif) 是首项为
是首项为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com