
题目列表(包括答案和解析)
已知函数![]() 和
和![]() 的图象关于原点对称,且
的图象关于原点对称,且![]() ,
,
(I)求![]() 的解析式;
的解析式;
(II)解不等式![]()
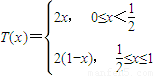
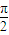 x))和y=sin(
x))和y=sin(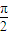 T(x))的解析式;
T(x))的解析式;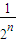 ]时,求y=Tn(x)的解析式;
]时,求y=Tn(x)的解析式;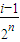 ,
,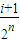 ](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(
](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(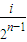 -x)恒成立.
-x)恒成立.
 时,求y=T4(x)的解析式;
时,求y=T4(x)的解析式; 时(i∈N*,1≤i≤15),都有
时(i∈N*,1≤i≤15),都有 恒成立.
恒成立.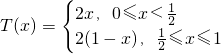
 x))和y=sin(
x))和y=sin( T(x))的解析式;
T(x))的解析式; ]时,求y=Tn(x)的解析式;
]时,求y=Tn(x)的解析式;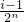 ,
,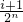 ](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(
](i∈N*,1≤i≤2n-1)时,都有Tn(x)=Tn(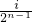 -x)恒成立.
-x)恒成立.已知函数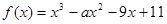 ,且
,且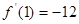 .
.
(I)求函数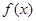 的解析式;
的解析式;
(II)求函数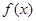 的单调区间和极值.
的单调区间和极值.
一、1――12 DBDCD CABAC DD
二、13.810 14. 6 15. 420 16. 
三、解答题
17.解(I)由 ,得
,得
由 ,得
,得
又
所以
(II)由正弦定理得
所以 的面积
的面积
18.解:

(I)
有 6中情况
6中情况
所以函数 有零点的概率为
有零点的概率为
(II)对称轴 ,则
,则

 函数
函数 在区间
在区间 上是增函数的概率为
上是增函数的概率为
 19.解:(I)证明:由已知得:
19.解:(I)证明:由已知得:




 (II)证明:取AB中点H,连结GH,FH,
(II)证明:取AB中点H,连结GH,FH,


 (由线线平行证明亦可)
(由线线平行证明亦可)
 (III)
(III)

 20.解(I)
20.解(I)


 (II)
(II)


 若
若 时,
时, 是减函数,则
是减函数,则 恒成立,得
恒成立,得


 (若用
(若用 ,则必须求导得最值)
,则必须求导得最值)
 21.解:(I)由
21.解:(I)由 ,得
,得
 解得
解得 或
或 (舍去)
(舍去)


 (II)
(II)


 22.(I)由题设
22.(I)由题设 ,及
,及 ,
, 不妨设点
不妨设点 ,其中
,其中 ,于点A 在椭圆上,有
,于点A 在椭圆上,有 ,即
,即 ,解得
,解得 ,得
,得
 直线AF1的方程为
直线AF1的方程为 ,整理得
,整理得
 由题设,原点O到直线AF1的距离为
由题设,原点O到直线AF1的距离为 ,即
,即
 将
将 代入上式并化简得
代入上式并化简得 ,得
,得
 (II)设点D的坐标为
(II)设点D的坐标为
 当
当 时,由
时,由 知,直线
知,直线 的斜率为
的斜率为 ,所以直线
,所以直线 的方程为
的方程为

 或
或 ,其中,
,其中,
 点
点 ,的坐标满足方程组
,的坐标满足方程组
 将①式代入②式,得
将①式代入②式,得
 整理得
整理得
 于是
于是
 由①式得
由①式得


 由
由 知
知 ,将③式和④式代入得
,将③式和④式代入得


 将
将 代入上式,整理得
代入上式,整理得
 当
当 时,直线
时,直线 的方程为
的方程为 ,
, 的坐标满足方程组
的坐标满足方程组

 ,所以
,所以 ,由
,由 知,
知,
 即
即 ,解得
,解得 ,这时,点D的坐标仍满足
,这时,点D的坐标仍满足
 综上,点D的轨迹方程为
综上,点D的轨迹方程为


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com