
题目列表(包括答案和解析)
设函数 ,其中a为正实数.
,其中a为正实数.
(l)若x=0是函数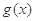 的极值点,讨论函数
的极值点,讨论函数 的单调性;
的单调性;
(2)若 在
在 上无最小值,且
上无最小值,且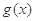 在
在 上是单调增函数,求a的取值范
上是单调增函数,求a的取值范
围;并由此判断曲线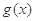 与曲线
与曲线 在
在 交点个数.
交点个数.
设函数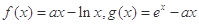 ,其中a为正实数.
,其中a为正实数.
(l)若x=0是函数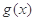 的极值点,讨论函数
的极值点,讨论函数 的单调性;
的单调性;
(2)若 在
在 上无最小值,且
上无最小值,且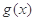 在
在 上是单调增函数,求a的取值范
上是单调增函数,求a的取值范
围;并由此判断曲线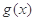 与曲线
与曲线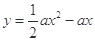 在
在 交点个数.
交点个数.
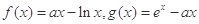 ,其中a为正实数.
,其中a为正实数.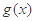 的极值点,讨论函数
的极值点,讨论函数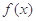 的单调性;
的单调性;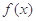 在
在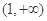 上无最小值,且
上无最小值,且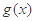 在
在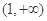 上是单调增函数,求a的取值范
上是单调增函数,求a的取值范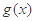 与曲线
与曲线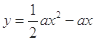 在
在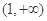 交点个数.
交点个数.| 3 | 2 |
| a |
| x |
| 1 |
| x |
| n+1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| n |
1.C 2.D 3.A 4.A 5.C 6.D 7.D 8.A 9.C10.D 11.B12.D
13.
14.
15.
16.
17
18.解:

⑴ 

 .
.
⑵ 函数
 在
在 上单调递增,
上单调递增,
在 上单调递减.
上单调递减.
所以,当 时,
时, ;当
;当 时,
时, .
.
故 的值域为
的值域为 .
.
19.解:由题意可知圆 的方程为
的方程为 ,于是
,于是 .
.
 时,设
时,设 ,
, ,则由
,则由 得,
得,
 ,
, . 所以
. 所以 的中点坐标为
的中点坐标为 .
.
又由 ,且
,且 ,可知直线
,可知直线 与直线
与直线 垂直,即直线
垂直,即直线 的斜率为
的斜率为 .
.
此时直线 的方程为
的方程为 ,即
,即 .
.
 时,同理可得直线
时,同理可得直线 的方程为
的方程为 .
.
故直线 的方程为
的方程为 或
或  .
.
20. 解:(Ⅰ)设这二次函数f(x)=ax2+bx (a≠0) ,则 f`(x)=2ax+b,由于f`(x)=6x-2,得
a=3 , b=-2, 所以 f(x)=3x2-2x.
又因为点 均在函数
均在函数 的图像上,所以
的图像上,所以 =3n2-2n.
=3n2-2n.
当n≥2时,an=Sn-Sn-1=(3n2-2n)-
=6n-5.
当n=1时,a1=S1=3×12-2=6×1-5,所以,an=6n-5 ( )
)
(Ⅱ)由(Ⅰ)
得知 =
= =
= ,
,
故Tn= =
=

= (1-
(1-
因此,要使 (1-
(1- )<
)< (
( )成立的m,必须且仅须满足
)成立的m,必须且仅须满足 ≤
≤ ,即m≥10,所以满足要求的最小正整数m为10.
,即m≥10,所以满足要求的最小正整数m为10.
21.解:⑴设
 ,∵不等式
,∵不等式 的解集为
的解集为
∴ ……… ①
……… ①  ……… ②
……… ②
又∵ 有两等根,
有两等根,
∴ ……… ③ 由①②③解得
……… ③ 由①②③解得  …………(5分)
…………(5分)
又∵ ,
,
∴ ,故
,故 .
.
∴ …………………………(7分)
…………………………(7分)
⑵由①②得 ,
,
∴ ,
,
 ……………………(9分)
……………………(9分)
∵ 无极值,∴方程
无极值,∴方程
 ,
,
解得 …………(12分)
…………(12分)
22.(1) ;
;

(2)
(3)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com