练习册

  • 练习册
  • 试题
    【查看更多】

     

    题目列表(包括答案和解析)

    本题满分14分）已知函数，，其中．w.w.w.k.s.5.u.c.o.m    

       （I）设函数．若在区间上不单调，求的取值范围；

       （II）设函数  是否存在，对任意给定的非零实数，存在惟一的非零实数（），使得成立？若存在，求的值；若不存在，请说明理由．

    查看答案和解析>>

    本题满分14分）
    ⑴已知cos（x+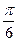）=，求cos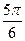（－x）+ cos2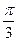（－x）的值。
    ⑵已知tanα=2，求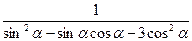

    查看答案和解析>>

    本题满分14分）已知向量  与  共线，设函数 ．

    （I） 求函数  的周期及最大值；

    （II） 已知锐角 △ABC 中的三个内角分别为 A、B、C，若有 ，边 BC＝，，求 △ABC 的面积．

     

    查看答案和解析>>

    本题满分14分）

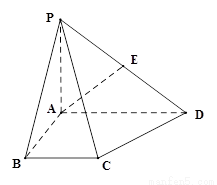
    四棱锥P-ABCD中，底面ABCD为直角梯形，，AD∥BC, AB=BC=2, AD=4,

    PA⊥底面ABCD，PD与底面ABCD成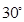角，E是PD的中点.

    （1）     点H在AC上且EH⊥AC，求的坐标；

    （2）     求AE与平面PCD所成角的余弦值；

     

    查看答案和解析>>

    本题满分14分）

    设命题p:函数是R上的减函数，命题q：函数在的值域为，若“p且q”为假命题，“p或q”为真命题，求的取值范围.

     

    查看答案和解析>>

    1．C  2．D  3．A  4．A  5．C  6．D  7．D  8．A 9．C10.D   11.B12.D

    13．

    14．

    15．

    16．  

    17

    18．解：

     ⑴ .

    ⑵ 函数在上单调递增，

    在上单调递减.

    所以,当时，；当时，.

    故的值域为.

    19．解：由题意可知圆的方程为，于是.

    时，设，，则由得,

    ，. 所以的中点坐标为.

    又由,且,可知直线与直线垂直，即直线的斜率为.

    此时直线的方程为,即.

    时,同理可得直线的方程为.

    故直线的方程为 或 .

    20. 解：（Ⅰ）设这二次函数f(x)＝ax2+bx (a≠0) ,则 f`(x)=2ax+b,由于f`(x)=6x－2,得

    a=3 ,  b=－2, 所以  f(x)＝3x2－2x.

    又因为点均在函数的图像上，所以＝3n2－2n.

    当n≥2时，an＝Sn－Sn－1＝（3n2－2n）－

    ＝6n－5.

    当n＝1时，a1＝S1＝3×12－2＝6×1－5，所以，an＝6n－5 （）

    （Ⅱ）由（Ⅰ）

    得知＝＝，

    故Tn＝＝

    ＝（1－

    因此，要使（1－）<（）成立的m,必须且仅须满足≤，即m≥10，所以满足要求的最小正整数m为10.

    21.解：⑴设，∵不等式的解集为

    ∴ ……… ①       ……… ②

    又∵有两等根，

    ∴……… ③     由①②③解得   …………（5分）

    又∵，

    ∴，故.

    ∴  …………………………（7分）

    ⑵由①②得，

    ∴，

    ……………………（9分）

    ∵无极值，∴方程

           ，

    解得  …………（12分）

    22.(1);

       (2)

       (3)

     

     

     


    同步练习册答案