
题目列表(包括答案和解析)
游乐场中的摩天轮匀速旋转,其中心O距地面40.5 m,半径40 m,若从最低点处登上摩天轮,那么你与地面的距离将随时间变化,5 min后到达最高点,在你登上摩天轮时开始记时.你能完成下面的问题吗?
(1)当你登上摩天轮2 min后,你的朋友也在摩天轮最低处登上摩天轮,请求出你的朋友与地面的距离y关于时间t的函数关系式;
(2)你和你的朋友与地面的距离差何时最大?最大距离差是多少?(sinα-sinβ=2cos![]() sin
sin![]() )
)
(3)如果规定每位游客乘坐摩天轮观景的时间是每次20 min,从你的朋友登上摩天轮的时间算起,什么时候你的朋友与地面的距离大于你与地面的距离?
已知函数![]() .(a,b为常数)
.(a,b为常数)
(Ⅰ)当a=1时,F(x)=0有两个不相等的实根,求b的取值范围;
(Ⅱ)若F(x)有三个不同的极值点0,x1,x2.a为何值时,能使函数F(x)在x1(或者x2)处取得的极值为b?
(Ⅲ)若对任意的a∈[-1,0],不等式F(x)≥-8在[-2,2]上恒成立,求b的取值范围.
(本题满分14分) 设函数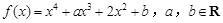 .
.
(Ⅰ)当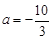 时,讨论函数
时,讨论函数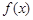 的单调性;
的单调性;
(Ⅱ)若函数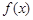 仅在x=0处有极值,试求a的取值范围;
仅在x=0处有极值,试求a的取值范围;
(Ⅲ)若对于任何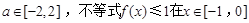 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
(本题满分14分) 设函数 .
.
(Ⅰ)当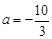 时,讨论函数
时,讨论函数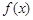 的单调性;
的单调性;
(Ⅱ)若函数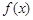 仅在x=0处有极值,试求a的取值范围;
仅在x=0处有极值,试求a的取值范围;
(Ⅲ)若对于任何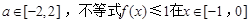 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
(本题满分14分) 设函数![]() .
.
(Ⅰ)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若函数![]() 仅在x=0处有极值,试求a的取值范围;
仅在x=0处有极值,试求a的取值范围;
(Ⅲ)若对于任何![]() 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
www..com
一、选择题 CAAD ABDAB CB
二、填空题  .
.
 .
.
 .
.
 .
.

三、解答题
 .
.





 的周期为
的周期为 ,最大值为
,最大值为 .
.
 由
由 得
得 ,
,
又 ,
, ,
,
∴ 或
或 或
或
∴ 或
或  或
或 
 .
. 显然事件
显然事件 即表示乙以
即表示乙以 获胜,
获胜,
∴

 的所有取值为
的所有取值为 .
.



∴ 的分布列为:
的分布列为:

3
4
5




数学期望 .
.
 .
. 当
当 在
在 中点时,
中点时, 平面
平面 .
.
 延长
延长 、
、 交于
交于 ,则
,则 ,
,
连结 并延长交
并延长交 延长线于
延长线于 ,
,
则 ,
, .
.
在 中,
中, 为中位线,
为中位线, ,
,
又 ,
,
∴ .
.
 ∵
∵ 中,
中,
∴ ,即
,即
又 ,
, ,
,
∴ 平面
平面 ∴
∴ .
.
∴ 为平面
为平面 与平面
与平面 所成二面
所成二面
角的平面角。
又 ,
,
∴所求二面角的大小为 .
.
 .
. 由题意知
由题意知 的方程为
的方程为 ,设
,设 ,
, .
.
联立 得
得 .
.
∴ .
.
由抛物线定义 ,
,
∴ .抛物线方程
.抛物线方程 ,
,
 由题意知
由题意知 的方程为
的方程为 .设
.设 ,
,
则 ,
, ,
,
∴
 .
.
由 知
知 ,
, ,
, ,
, .
.
则
∴当 时,
时, 的最小值为
的最小值为
 .
.
 .
. ∵
∵
 ,
,
∴ .
.
∴
∴
即
∴ s
s


 时,也成立
时,也成立
∴

 ,
,
∴

∴


∵
 ,
,
又




∴
 .
.
 ,
,
∵ 在
在 上单调,
上单调,
∴ 或
或 在
在 上恒成立.
上恒成立.
即 或
或 恒成立.
恒成立.
 或
或 在
在 上恒成立.
上恒成立.
又 ,
,
∴ 或
或 .
.
 由
由 得:
得:
 ,
,
化简得
当 时,
时, ,
, ,
,
∴
又 ,
,
∴
当 时,
时, ,
,
综上,实数 的取值范围是
的取值范围是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com